几何大变形圆柱壳非线性振动分析：渐近摄动法

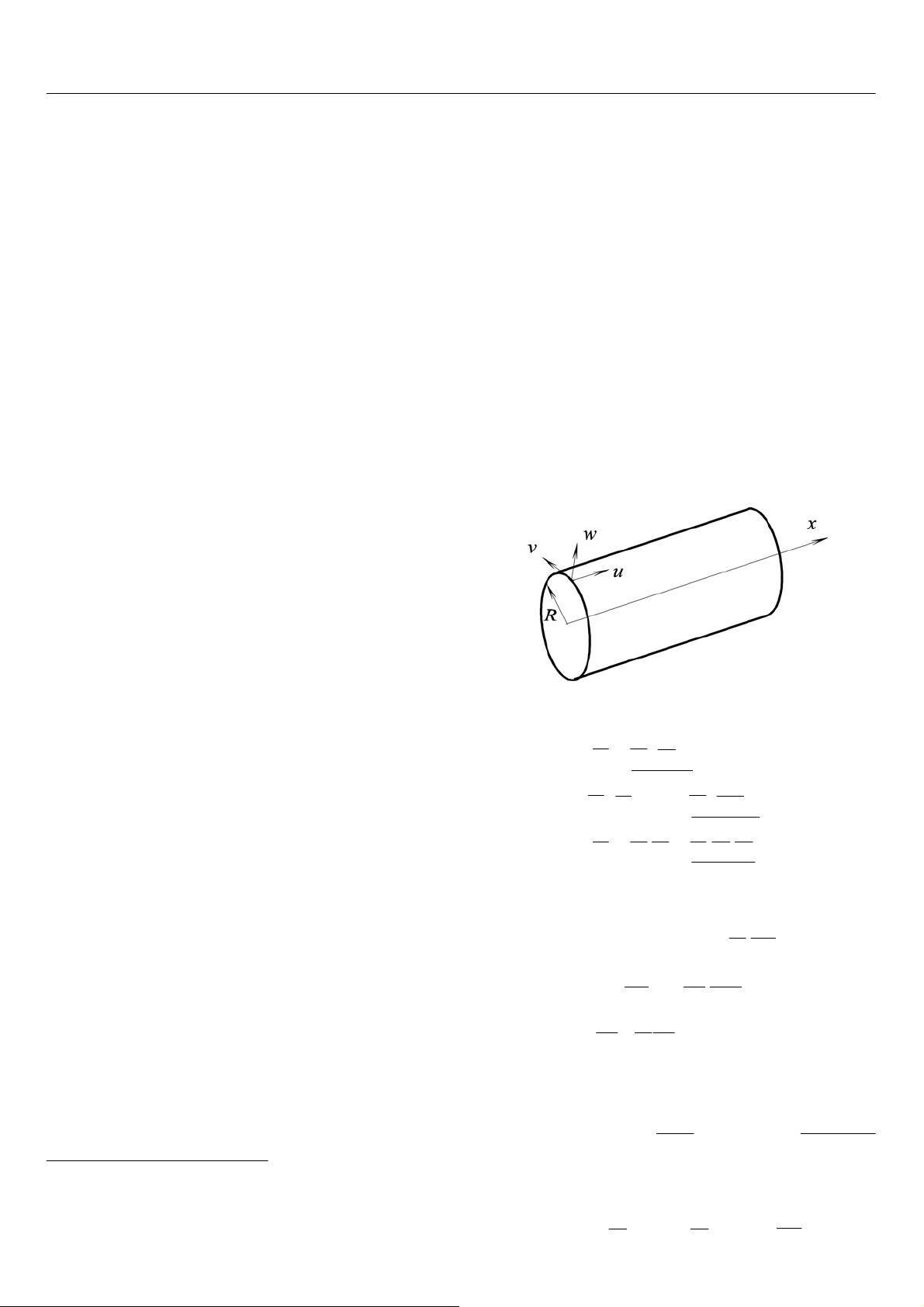
"该资源是一篇2007年的学术论文，主要探讨了圆柱壳在大几何变形下的非线性振动问题，采用渐近摄动法来求解非线性频率。研究背景是薄壁圆柱壳在航天、航空等领域的重要应用，以及在复杂工况下可能产生的非线性振动现象。作者通过Donnells简化壳理论建立了包含位移三次项的非线性频率方程，并利用幂级数展开和耦合代数方程来求解。通过Galerkin方法进行解耦正交处理，忽略了永年项，分析了内共振现象。最后，通过摄动法得到了非线性频率的一次近似解，揭示了几何非线性对振动频率的影响，以及频率与节径数、初始位移的关系。文中还引用了前人关于非线性振动的研究，并指出I.V. Andriov的渐近摄动法等相关工作作为参考。" 这篇论文详细介绍了如何利用渐近摄动法解决薄壁圆柱壳的大几何变形导致的弱非线性振动问题。首先，研究者基于Donnells简化壳理论，建立了一个考虑几何非线性的薄壁圆柱壳振动模型，这个模型中包含了位移的二次和三次非线性项。随后，他们将位移和频率以非线性参数的幂级数形式展开，并通过设置同次幂非线性项系数相等来构建一系列耦合代数方程。 为了进一步求解这些方程，研究人员采用了Galerkin方法进行解耦正交处理，这有助于简化问题并忽略那些不重要的永年项。在处理过程中，他们特别关注了实数根，以避免各阶频率对应的振幅间的内共振现象。通过引入小参数，然后运用摄动法，他们成功地求解出非线性频率的一次近似值。这种方法揭示了几何非线性如何导致薄壁圆柱壳的硬化效应，即非线性频率上升，同时也探讨了线性和非线性频率与节径数、初始位移之间的定量关系。 此外，论文还引用了其他学者的工作，比如I.V. Andriov的渐近摄动法，以及A.H. Nayfeh、M. Amabili和F. Pelliano关于无水和含水薄壁圆柱壳非线性振动的研究，这些都为当前的研究提供了理论基础和对比分析。 这篇论文对于理解和预测在实际工程应用中，如航天、航空、石油和海底管道等领域，薄壁圆柱壳的非线性振动特性具有重要的理论价值和实践指导意义。它不仅提供了一种有效的分析方法，也为后续的相关研究奠定了基础。