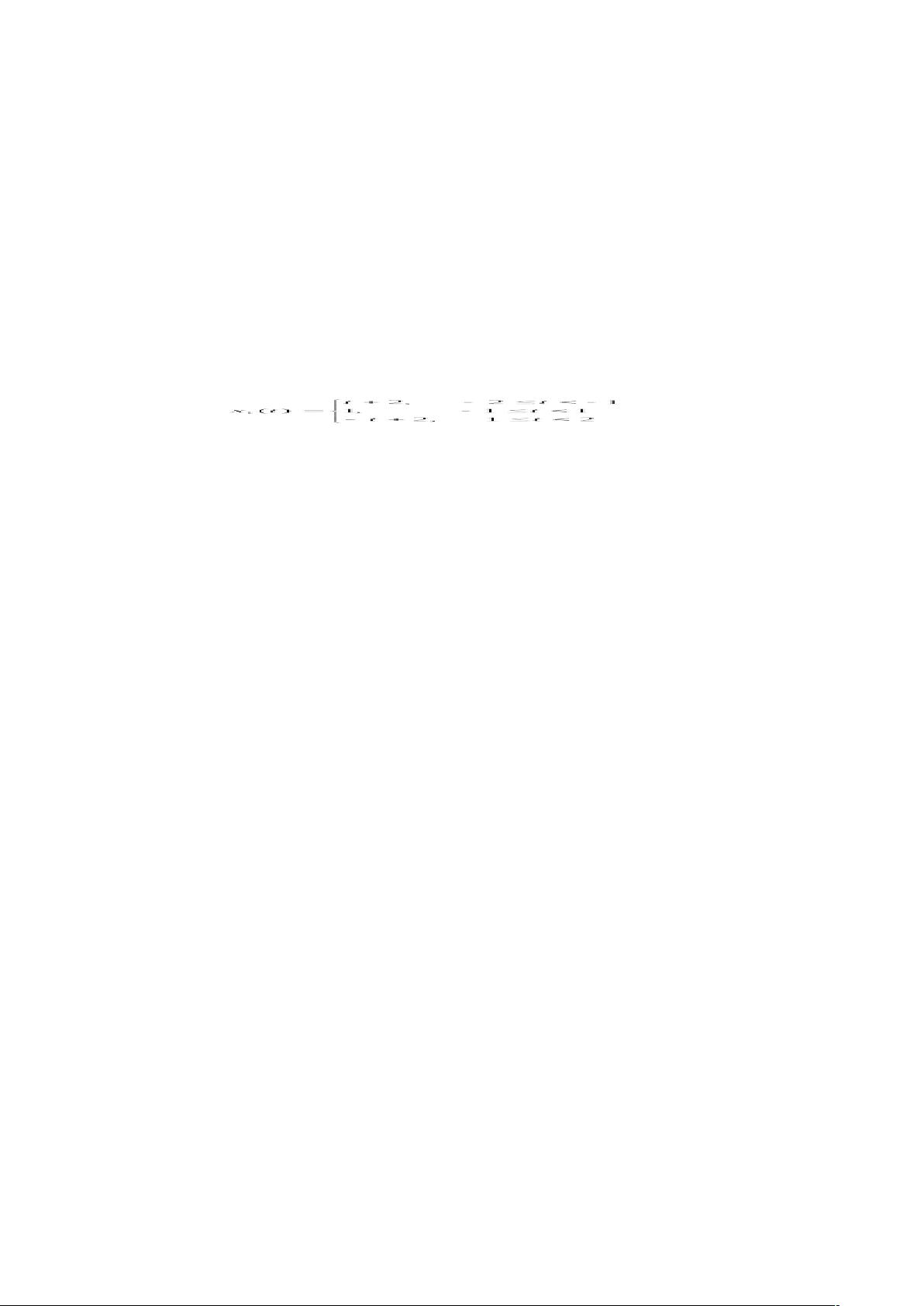MATLAB实现非周期信号傅立叶变换分析

"非周期信号的傅立叶变换分析" 非周期信号的傅立叶变换是信号处理中的核心概念，它允许我们将一个有限时间内的信号分解为不同频率成分的叠加，从而揭示信号在频域内的特性。这个分析对于理解和设计电子系统、通信系统以及图像处理等领域至关重要。 在实验4中，我们关注的是非周期信号的傅立叶变换分析。实验目的是让学生们熟悉非周期信号频谱的特点以及如何使用MATLAB进行分析。具体包括以下三个关键点： 1. 理解连续非周期信号的频谱特性：非周期信号的频谱是离散的，每个频率成分对应于信号的一个特定幅度，这些幅度共同构成了信号的整体形状。 2. 掌握MATLAB中傅立叶变换的实现：MATLAB提供了两种方法来计算傅立叶变换，一种是数值运算方法，另一种是符号运算方法。数值运算方法通常用于实际数据，而符号运算方法适用于理论分析，可以得到解析表达式。 3. 学习傅立叶变换的性质：包括线性性、共轭对称性、尺度和位移等基本性质，并了解如何在MATLAB中应用这些性质。 实验内容包括对给定时限信号x1(t)的分析。x1(t)是一个由阶跃函数构成的复杂信号，其傅立叶变换可以通过数值和符号运算进行计算。MATLAB程序Q4_1首先定义了信号x1(t)，然后使用`exp(-j*t'*w)`来表示傅立叶变换的卷积性质，乘以采样时间T是为了归一化。通过`abs(X)`和`angle(X)`分别获取幅度谱和相位谱。 数值运算部分使用了MATLAB内置的`fourier`函数，而符号运算部分则利用`sym`函数创建符号表达式，并调用`fourier`函数进行傅立叶变换。实验结果通过`subplot`函数绘制了时域波形、幅度谱和相位谱，帮助理解信号的频域特性。 此外，实验还涉及了单边指数信号的傅立叶变换，这类信号的傅立叶变换具有特殊的解析形式，通常涉及到复指数函数和 sinc 函数。 总结起来，非周期信号的傅立叶变换分析是一个深入理解信号本质和频域特征的过程，通过MATLAB这样的工具，我们可以直观地探索信号的频谱结构，这对于工程应用和理论研究都极其重要。