四元数与三维旋转：直观解析

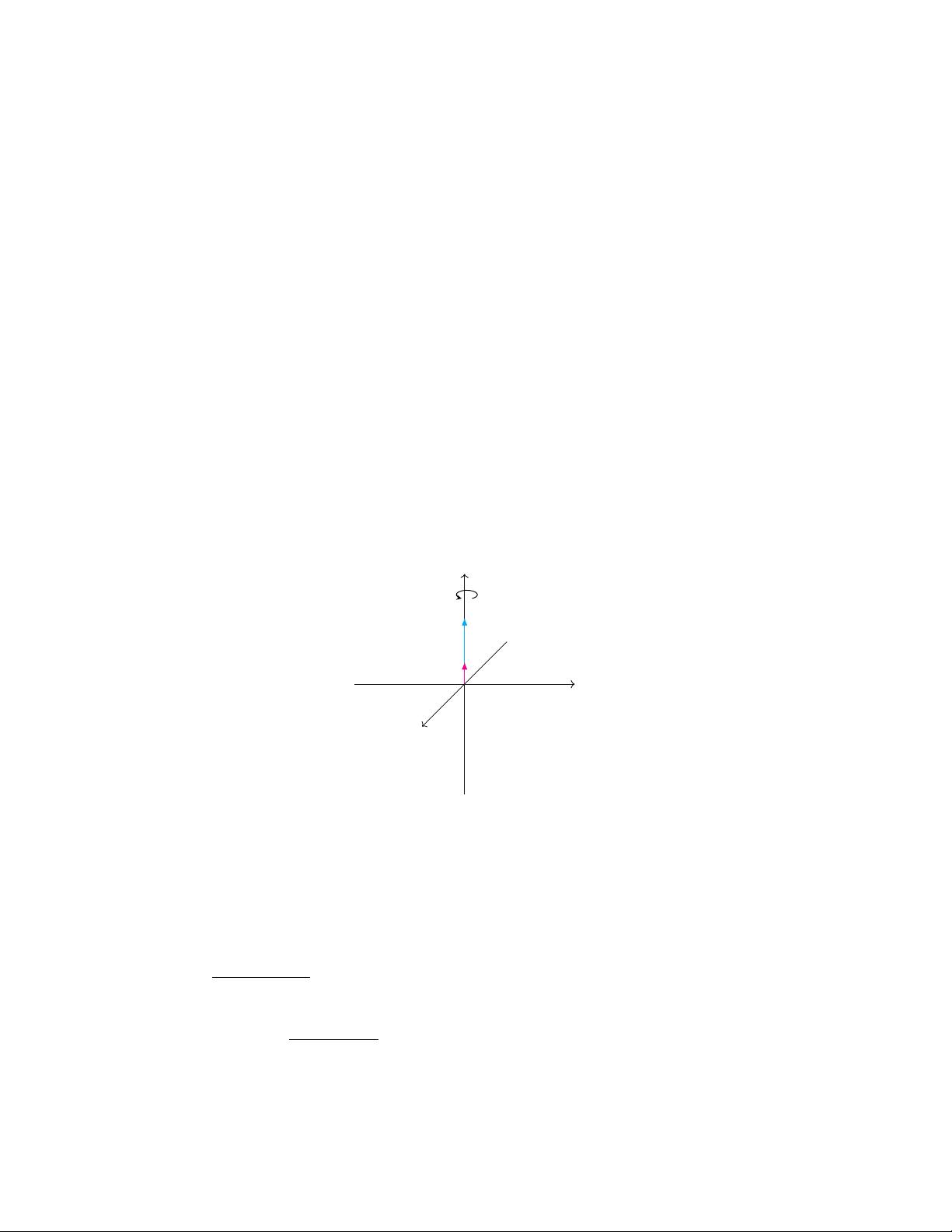
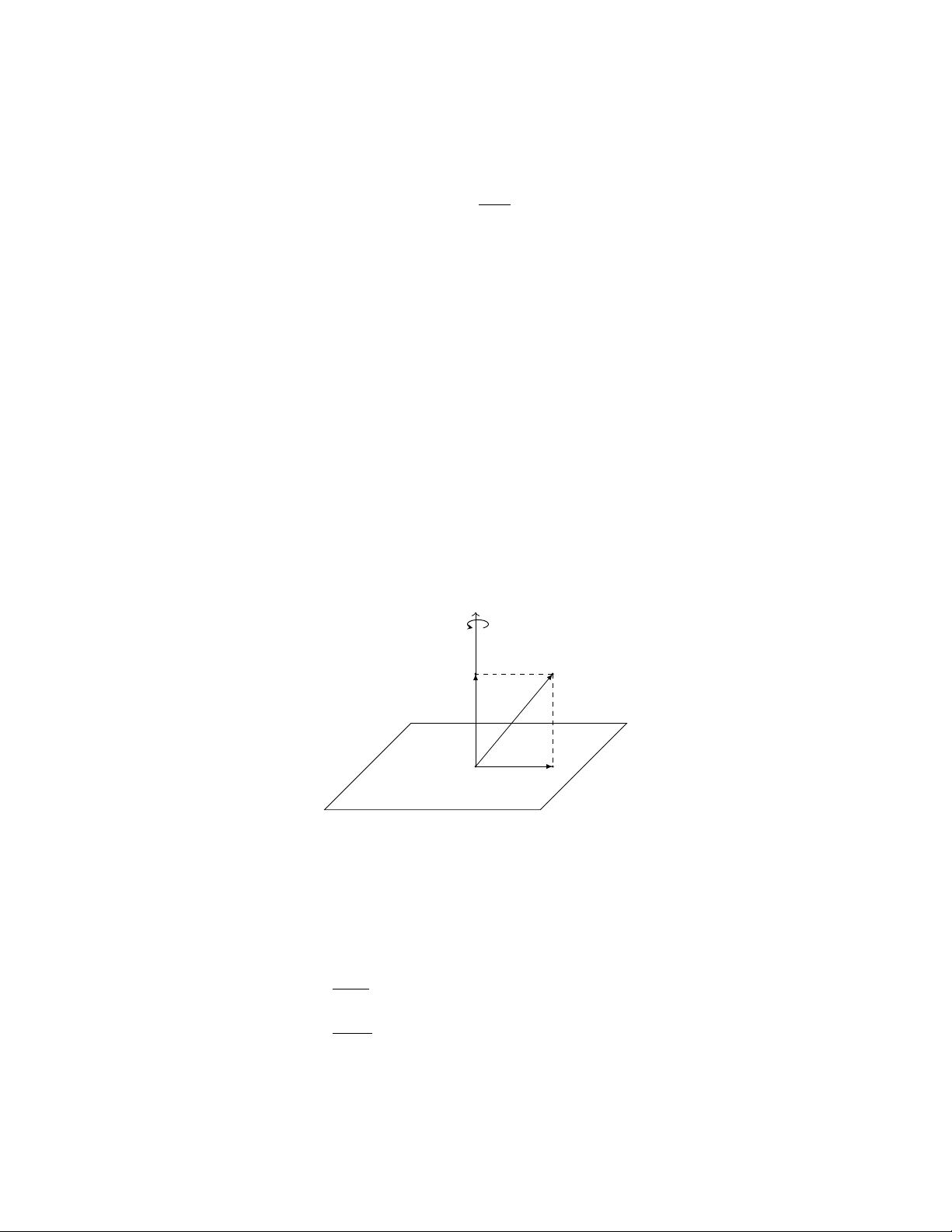
"该资源是一篇关于四元数与三维旋转的详细文章，作者Krasjet旨在探讨四元数在3D旋转中的应用，以及如何用几何学和线性代数的知识来理解这一概念。文章包含MATLAB/Octave的示例代码和相关动画，可在GitHub上找到。作者提醒读者，文章可能不适用于物理学或抽象代数的学习者，但提供了拓展阅读资源。文章以CCBY-NC-SA4.0协议发布，要求署名和非商业使用。" 四元数是一种扩展复数的概念，用于解决三维空间中的旋转问题。在进入四元数的讨论之前，文章首先简要介绍了复数，因为两者之间有许多相似性。复数由实部和虚部构成，形式为\( z = a + bi \)，其中\( a, b \)是实数，\( i \)是虚数单位，满足\( i^2 = -1 \)。复数可以看作是在二维平面上的一种向量表示，其旋转可以通过复数乘法实现。 四元数（Quaternion）是由三个虚部（Imaginary Units）\( j, k \)扩展复数概念而来的，除了实部外，还有三个虚部分量，形式为\( q = w + xi + yj + zk \)，其中\( w, x, y, z \)都是实数。与复数不同的是，四元数的虚部满足特定的乘法规则，即\( ij = k, jk = i, ki = j \)，同时这些关系遵循反交换律（Anti-commutative），即\( ji = -k, kj = -i, ik = -j \)。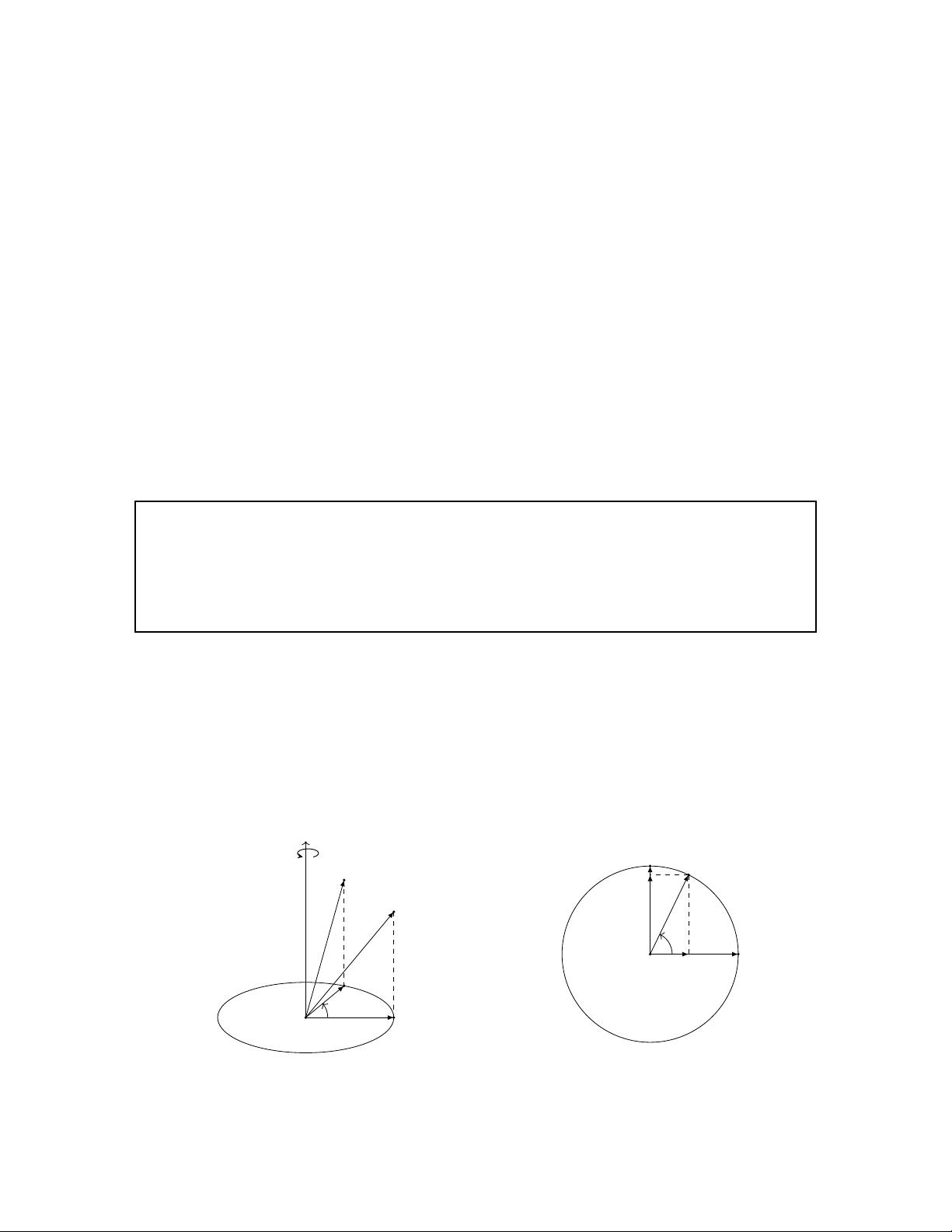 四元数与三维旋转的关系在于，它们提供了一种简洁且无旋积（Non-commutative）的方式去描述空间中的旋转。在计算机图形学中，四元数被广泛应用于表示和计算物体的旋转状态。相比于欧拉角（Euler Angles）和旋转矩阵（Rotation Matrix），四元数避免了万向锁（Gimbal Lock）问题，即在某些情况下，欧拉角可能会丢失一维度的自由度。 通过四元数乘法，可以轻松地将两个旋转合并，这在处理连续的旋转动作时非常有用。四元数的逆（Inverse）代表相反的旋转，其计算相对简单，为\( q^{-1} = \frac{\bar{q}}{|q|^2} \)，其中\( \bar{q} \)是四元数的共轭，\( |q| \)是四元数的模（Magnitude）。四元数的模保持旋转的幅度不变，而共轭确保旋转方向相反。 文章中可能包含MATLAB/Octave代码示例和动画，这些可视化工具有助于读者直观地理解四元数旋转的效果。通过这些代码，读者可以亲手操作四元数，进一步加深对四元数旋转的理解。 在计算机图形学中，四元数通常用于游戏开发、3D建模和模拟等场景，它们在数学上的优雅性和计算效率使其成为处理三维旋转的理想工具。尽管四元数的理论较为抽象，但借助几何学和线性代数的知识，我们可以更好地理解和应用这一概念。对于想要深入学习四元数的读者，作者提供的拓展阅读资源可能是个不错的选择。