四元数与三维旋转详解

“quaternion.pdf”是一份详细讲解四元数及其在三维旋转中应用的资料，适合游戏开发中学习四元数旋转的读者。作者通过几何学和线性代数的基础知识，清晰地阐述了四元数与三维旋转的关系，同时提供了MATLAB/Octave的示例代码和相关动画。 四元数是一种扩展复数的概念，广泛应用于计算机图形学和游戏开发中的3D旋转表示。在介绍四元数之前，首先回顾复数的基本概念。复数由实部和虚部构成，形式为z=a+bi，其中i是虚数单位，满足i²=-1。复数可以看作是在二维平面上的向量，其旋转可以通过乘以单位复数e^(iθ)实现，这里的θ是旋转角度。 接下来进入四元数的世界，四元数Q=q0+q1i+q2j+q3k的形式类似于复数，但增加了两个额外的虚部j和k。这里i²=j²=k²=-1，同时ij=k，jk=i，ki=j，这组成了四元数的非交换性质。四元数的这种结构允许它表示三维空间中的旋转，而不仅仅是平面旋转。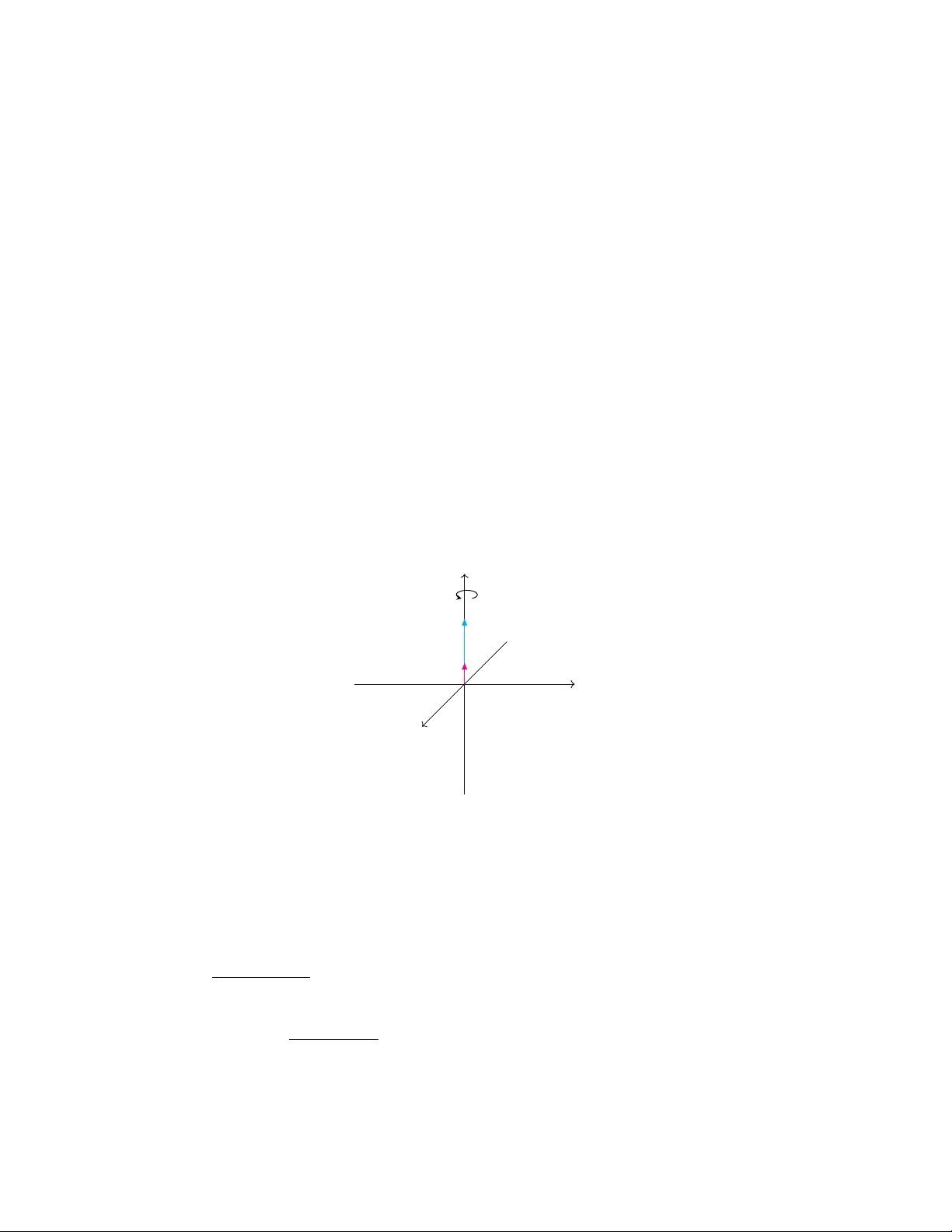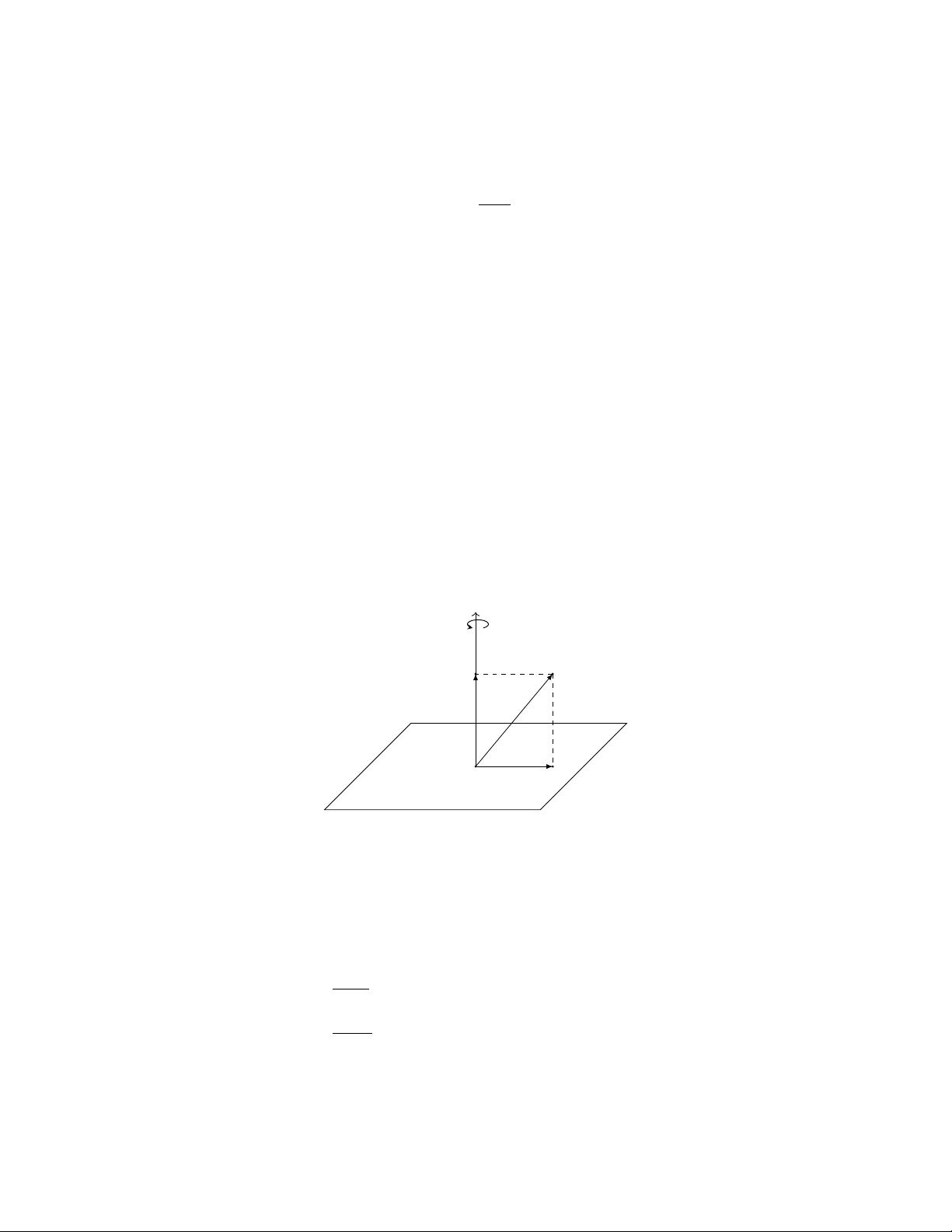 在3D旋转中，四元数提供了一种有效且无万向锁问题的解决方案。传统的欧拉角可能会遇到万向锁问题，即在某些情况下无法连续、平滑地表示旋转。四元数通过一个标量部分（q0）和一个三元向量部分（q1, q2, q3）来描述旋转，其中标量部分表示旋转的幅度，向量部分表示旋转轴的方向。四元数的乘法可以表示复合旋转，通过单位四元数（模长为1的四元数）乘法，可以轻松地将多个旋转合并。 四元数旋转的计算通常涉及四元数与向量的乘法。对于一个3D向量v，其在四元数Q表示的旋转下的变换可以用以下公式表示： v' = Q * v * conj(Q) 其中，conj(Q)是Q的共轭四元数，即q0不变，虚部取相反数。这个公式可以确保旋转前后保持向量长度不变，符合旋转的特性。 文章中可能还包含了实际编程中的四元数操作示例，如MATLAB/Octave代码，帮助读者更好地理解和应用这些理论知识。此外，作者鼓励读者发现错误或提出建议，提供了一个反馈渠道。 这份资料深入浅出地介绍了四元数与三维旋转的关系，是学习游戏开发中四元数应用的好资源。通过阅读，读者不仅能理解四元数的数学原理，还能掌握如何在实际项目中运用它们进行3D对象的旋转操作。