局部量化码直方图：一种纹理分类新方法

47 浏览量更新于2024-08-28 收藏 2.64MB PDF 举报

“LocalQuantizationCodehistogram用于纹理分类的研究论文，由Yang Zhao, Rong-Gang Wang, Wen-Min Wang, Wen Gao等人撰写，发表于Hebei University of Technology和Peking University Shenzhen Graduate School。” 在该研究论文中，作者提出了一种用于纹理分类的有效局部算子，称为Local Quantization Code (LQC)。传统的局部二进制模式（Local Binary Pattern, LBP）可以视为具有两个量化级别的局部量化方法，即0和1。LBP的某些变体已经显示，增加局部量化级别可以增强局部判别能力。因此，作者提供了一个简单且统一的框架来验证不同局部量化级别的性能。 LQC的主要创新之处在于，它将位于不同量化级别的像素分开处理。这可能意味着每个像素的表示更精细，从而提供了更多的纹理特性信息。通过使用多级量化，LQC能够捕捉更复杂的纹理结构，这可能比传统的二值化方法（如LBP）更有利于纹理的区分和识别。作者对LBP的扩展表明，量化级别的增加可以提供更丰富的局部特征描述，这对于纹理分类任务至关重要。在实际应用中，纹理分类广泛应用于图像分析、视频监控、医学影像处理等领域，提高分类准确性和效率对于这些应用来说非常关键。此外，文章可能还涉及了实验设计和结果分析，对比了LQC与其他现有的纹理描述符（如LBP及其变体）的性能。通过实验，作者可能证明了LQC在保持较低计算复杂度的同时，能提供更好的分类性能，这对于实时系统尤其重要。关键词：局部二进制模式，纹理分类，局部量化这篇论文贡献了一种新的纹理分类技术，通过改进局部量化策略，提高了纹理描述的准确性，为后续的计算机视觉研究和应用提供了新的工具。其潜在的应用价值在于提升图像分析的精度，特别是在需要快速和准确识别纹理信息的场景中。

thresholds are ﬁxed, the pixels on the local neighbor set are

classiﬁed into different quantization levels. The number of

neighbor pixels located at the ith quantization level (q

) is then

counted as follows:

p ¼ 1

Lðg

g

Þ; LðxÞ¼

1; if

r x

r σ

i þ 1

0; else

(

ð2Þ

where g

represents the gray value of the center pixel and g

(p¼1,

…,P) denotes the gray value of the neighbor pixel on a circle

neighbor set, and

is the ith quantization threshold. As in [9], the

neighbors that do not fall in the center of pixels are estimated by

bilinear interpolation. Obviously, computing the q

is equal to

count the number of the neighbor pixels that are quantized into

the ith level.

After the q

at each local quantization level is calculated, we can

deﬁne the Local Quantization Code (LQC) as follows:

LQC ¼

i ¼ 1

 10

i  1

ð3Þ

where q

is the number of neighbor pixels at quantization level i,

and Q represents the total number of the neighbor quantization

levels.

The center pixel, which expresses the local gray level, also has

discriminative information. Therefore the proposed LQC is also

combined with the global quantization level of the central pixel:

LQC ¼ q

 10

i ¼ 1

 10

i  1

ð4Þ

where q

represents the quantization level of the central pixel. In

this paper, the central pixel is quantized by equally splitting the

gray level histogram. The proposed LQC encoding scheme adopts a

decimal system coding rather than commonly used binary system

coding, thus the central quantization level q

can be set from 0 to

9. Different to the neighbor pixels, the gray value of central pixel is

quantized by means of global quantization method instead of local

quantization. That is because q

is supposed to describe the level of

local gray value among the whole image.

Fig. 4 illustrates the encoding process of the LQC at (R¼ 1, P¼8).

Each cubic column denotes a pixel and the height of the cubic

column represents the gray value of corresponding pixel. In Fig. 4,

gray value of neighbor pixels is quantized into 4 levels. Then the

number q

(i¼1,…,4) of neighbor pixels located at each level is

counted. There are 1, 2, 2, 3 pixels located at 1st, 2nd, 3th, and 4th

level, respectively. Finally, numbers of pixels at different levels are

combined to form the LQC code 122. We omit the last number 3 at

1st level to reduce the feature size, since the total number of

neighbor pixels is ﬁxed (1 þ 2þ 2þ 3¼ 8).

It is obvious that the LQC can accurately characterize the local

structure by means of more quantization levels than traditional

LBP. As shown in Fig. 5, different local structures may have the

same LBP code. But their LQC codes are quite different from each

other. Note that the LQC merely counting the number of pixels at

different levels and thus is strictly invariant to rotation. As a result,

the LQC encoding is very suitable for the rotation invariant texture

classiﬁcation scenario.

In this paper, the neighbor number P at radius 1 is set as 8, i.e.,

(R¼1, P¼8), therefore the value of each q

can be nine value (0–8).

When the radius of the neighbor set enlarged, the value of each q

is still quantized into nine values (0-8) so that the decimal system

based Eq. (4) can be used at larger radiuses. For example, the value

range of q

is 0 to 16 when the radius is 2, and this q

is then

directly quantized into nine levels (0–8).

After the Local Quantization Code of each pixel is calculated, a

histogram is built to represent the texture image. It should be

noted that although the size of LQC histogram is 10

with quan-

tization level L, many bins of the histogram are always zeros. That

is because there are only ﬁnite neighbor pixels to be encoded. For

example, if the q

at the quantization level 4 is 8 with (R¼ 1, P¼ 8),

the LQC code only can be ‘800’ since there are total 8 neighbor

pixels. The rest codes ‘801’ to ‘899’ are thus insigniﬁcant and we

can simply remove these meaningless all-zeros-bins from the ﬁnal

histogram. After removing the all-zeros-bins, the sizes of LQC

histograms are 9, 45, 165, 495 with (q

¼0, R ¼1, P ¼8) for quan-

tization level of 2, 3, 4, 5, respectively.

In conventional LBP, the gray value of local central pixel is used

as local threshold directly. It is clear that the ﬁxed artiﬁcial

threshold is not robust to discontinuous and non-uniform illumi-

nation transformations, while the local difference is relatively

more insensitive to illumination transformations. Hence, we adopt

the average local difference to set the series of quantization

thresholds instead of ﬁxed artiﬁcial thresholds. A base-threshold

is computed as the average difference of local neighbors on the

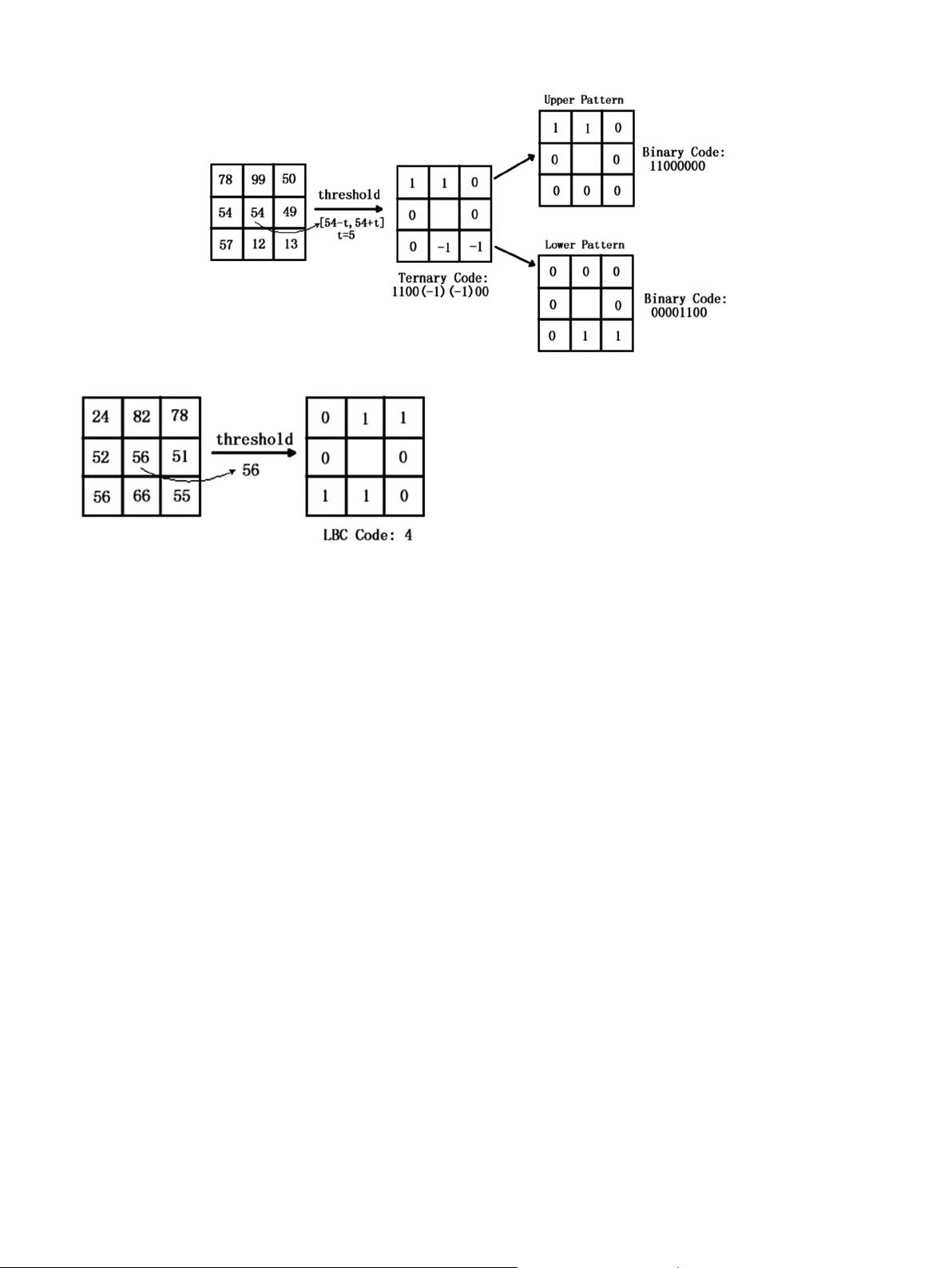
Fig. 2. Illustration of the LTP (P¼8, R¼1).

Fig. 3. The illustration of the LBC (P¼8, R¼1).

Y. Zhao et al. / Neurocomputing 207 (2016) 354–364356

剩余10页未读，继续阅读

weixin_38665944

粉丝: 6
资源: 914

局部量化码直方图：一种纹理分类新方法

Blur Insensitive Texture Classification

Rotation invariant texture classification using LBP variance (LBPV)

quantization

pytorch的Quantization介绍

integer quantization for deep learning inference: principles and empirical e

数字图像的quantization parameters有哪些

quantization bit 对信号量化的影响

如何得到一张数字图像的quantization parameters

python实现得到一张数字图像的quantization parameters

deep learning toolbox model quantization library 下载

最新资源