Python实现高斯判别分析：多元正态分布与GDA算法详解

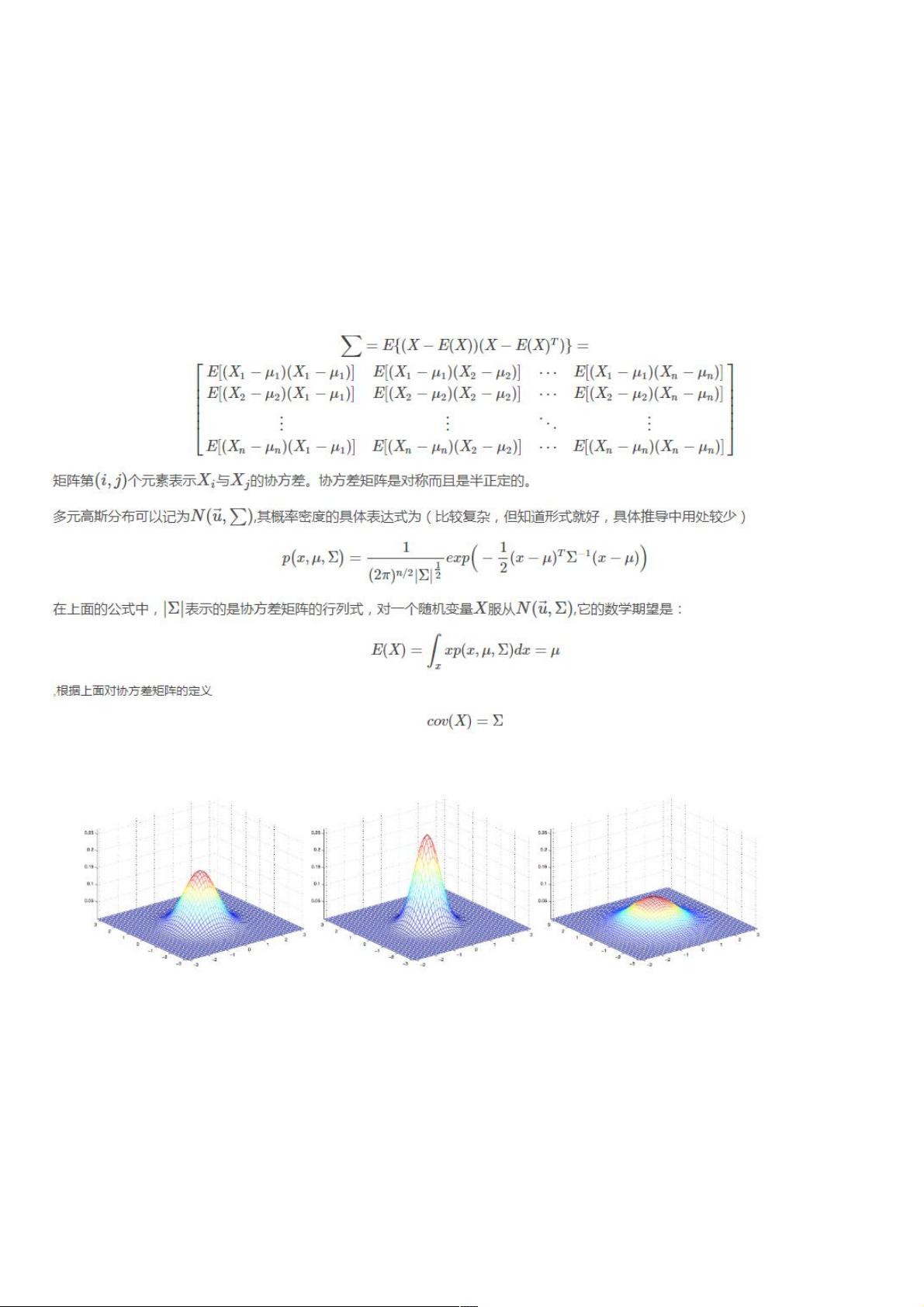
高斯判别分析算法（GDA）是一种在统计学和机器学习中广泛应用的分类方法，它属于生成学习的一种。在Python中实现该算法时，我们基于以下核心概念： 1. 多元正态分布：算法的核心假设是，给定类别y，输入数据X服从多元正态分布，即每个样本点X的每个特征独立地服从均值μ和协方差矩阵Σ的正态分布。多元正态分布有两个关键参数：μ（均值向量，每个维度的期望值）和Σ（协方差矩阵，衡量不同特征之间的线性相关性）。 2. 协方差矩阵：它是衡量随机变量之间关系的重要工具，定义为列向量X的期望值E(X)的偏差的平方和。协方差矩阵Σ是正定的，确保了分布的唯一性。Σ的大小和结构会影响数据点在高维空间中的分布形状，如标准正态分布（Σ=I，单位矩阵）表示所有特征间相互独立，而Σ变大或变小则会改变数据的集中程度。 3. 判别学习与生成学习：GDA属于判别学习，与之相对的是生成学习，后者假设p(y|x)（类别给定特征的概率）是易于建模的，而GDA则假设p(x|y)（特征给定类别的概率）更为直观。 4. 似然函数：算法的目标是最大化似然函数L，通过估计μ和Σ来找到最佳的分类决策边界。这通常通过求解优化问题来完成，涉及到计算梯度并更新参数。 5. Python实现：在实际编程中，例如使用Python，可能需要通过numpy库来处理矩阵运算，计算概率密度函数。但代码实现可能存在错误，比如矩阵操作不正确，特别是在处理二维数据时简化公式。通过可视化，我们可以直观地理解算法如何将不同协方差矩阵对应的高斯分布应用于分类任务。 在实践中，GDA可以用于降维、特征选择和分类，尤其是在处理连续型输入数据时。通过理解并应用这些原理，开发者可以在Python中构建并调试高斯判别分析模型，以解决实际问题。