MATLAB实现有限差分法解静电场边值问题

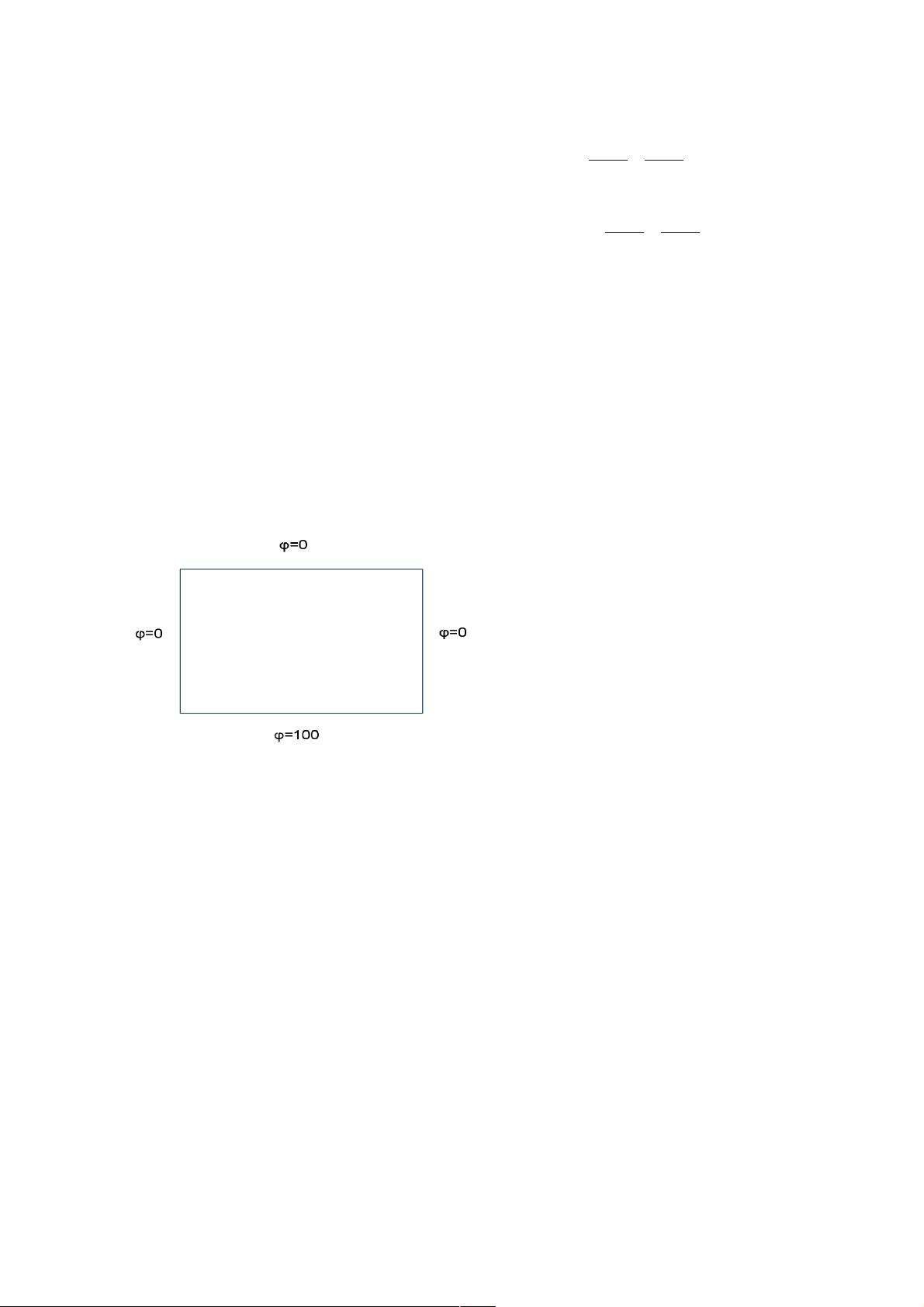
"有限差分MATLAB在解决静电场边值问题的应用" 有限差分法是一种在数值分析中常用于求解偏微分方程(PDEs)的数值方法，尤其适用于处理那些无法得到解析解的实际问题。在MATLAB环境下，这种方法能够有效地将偏微分方程转化为线性方程组，进而通过迭代法找到数值解。 本文作者王宁远通过MATLAB程序实现了有限差分法来解决静电场的边值问题，具体涉及的是泊松方程和拉普拉斯方程。泊松方程是描述静电场的一个基本方程，其形式为∇²U = ρ，其中∇²是拉普拉斯算子，U是电势函数，ρ是电荷密度。在二维或三维空间中，这个方程描述了电势如何受电荷分布的影响。 有限差分法的核心思想是将连续的物理空间离散化为一系列离散点，然后用差分近似导数。例如，一阶差分可以近似微分，如 f'(x) ≈ (f(x+h) - f(x))/h，当h趋于0时，这等价于导数的定义。二阶差分则用于更精确地近似导数的平方，例如 f''(x) ≈ (f(x+h) + f(x-h) - 2f(x))/h²，这对应于拉普拉斯算子的一部分。 在泊松方程的上下文中，通过二阶差分，可以将拉普拉斯算子在每个离散点上的作用表示为相邻点的函数差。在MATLAB中，可以通过建立一个矩阵来存储这些离散点上的电势值，进而构建一个线性方程组，其中每个方程对应于泊松方程在特定离散点的差分近似。通常，这种线性方程组的规模会很大，因此需要迭代法（如高斯-塞德尔迭代法或雅可比迭代法）来求解。 作者讨论了优化迭代法的策略，比如调整步长h、预条件技术以及迭代次数的控制，以提高求解效率和精度。此外，他还应用这种方法重新计算了某个闪电模拟问题，改进了模型，并对比了与前人研究的不同之处。 通过有限差分法，MATLAB不仅可以用来求解静电场问题，还可以应用于流体力学、热传导、弹性力学等领域中的PDEs。这种方法虽然不能给出解析解，但其数值解在实际工程和科学计算中具有很高的实用价值。