傅里叶级数与变换在数字信号处理中的应用

"《Fourier Series, Fourier Transforms, and The DFT》是W.K. Jenkins撰写的一章，收录在由Vijay K. Madisetti和Douglas B. Williams编辑的《Digital Signal Processing Handbook》中，由CRC Press LLC于1999年出版。本书章节涵盖了傅里叶级数、傅里叶变换以及离散傅里叶变换（DFT）的核心概念和技术。" 本章首先介绍了傅里叶分析的基本概念，它是信号处理和工程领域中的基础工具。傅里叶级数用于表示连续时间周期性信号，通过将复杂信号分解为正弦和余弦函数的无限级数，简化了对信号的理解和分析。其中，章节分别讨论了指数形式的傅里叶级数和三角形式的傅里叶级数，并阐述了级数的收敛性质。 接着，章节进入了经典傅里叶变换的领域，这是用于分析非周期连续时间信号的重要工具。这里讨论了连续时间傅里叶变换的特性，包括其对信号频谱的表示、连续时间采样模型的傅里叶变换、周期连续时间信号的傅里叶变换，以及广义复傅里叶变换。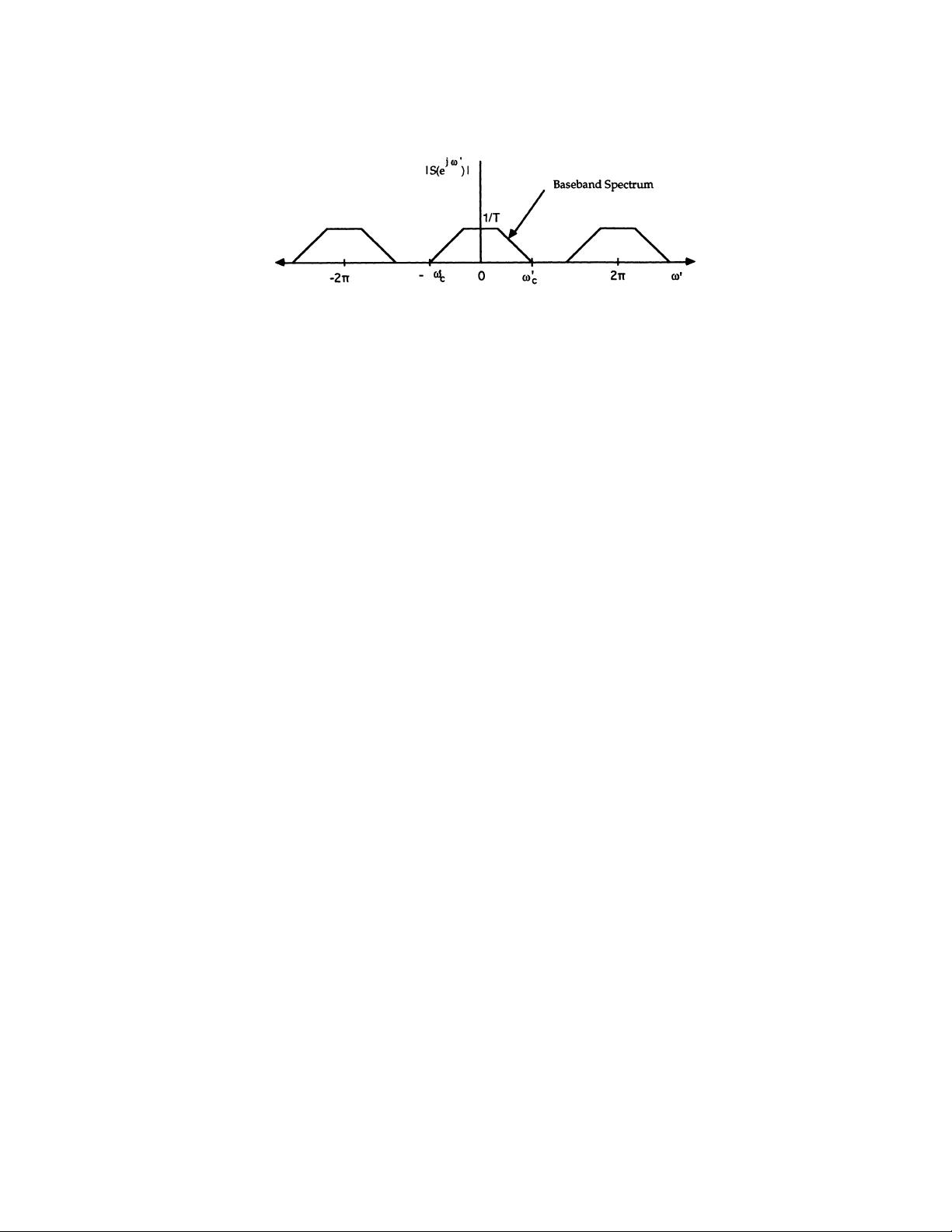 然后，作者转向了离散时间傅里叶变换（DTFT），它是离散信号分析的基础。DTFT的性质及其与连续时间谱的关系被详细阐述，强调了离散信号与连续信号之间的转换。 重点章节之一是关于离散傅里叶变换（DFT），它在数字信号处理中扮演着核心角色。DFT的特性，如其作为离散信号的傅里叶级数，以及在实时滤波应用中的傅里叶块处理，被深入探讨。此外，快速傅里叶变换（FFT）算法的介绍，展示了如何高效地计算DFT，极大地提高了计算效率。 最后，作者给出了傅里叶分析家族树，概述了各种变换之间的关系，这有助于读者理解不同变换在不同情境下的适用性和关联性。 这一章提供了对傅里叶分析全面而深入的洞察，对于学习和理解信号处理、通信、图像处理等领域的学生和专业人士来说，是一份宝贵的参考资料。