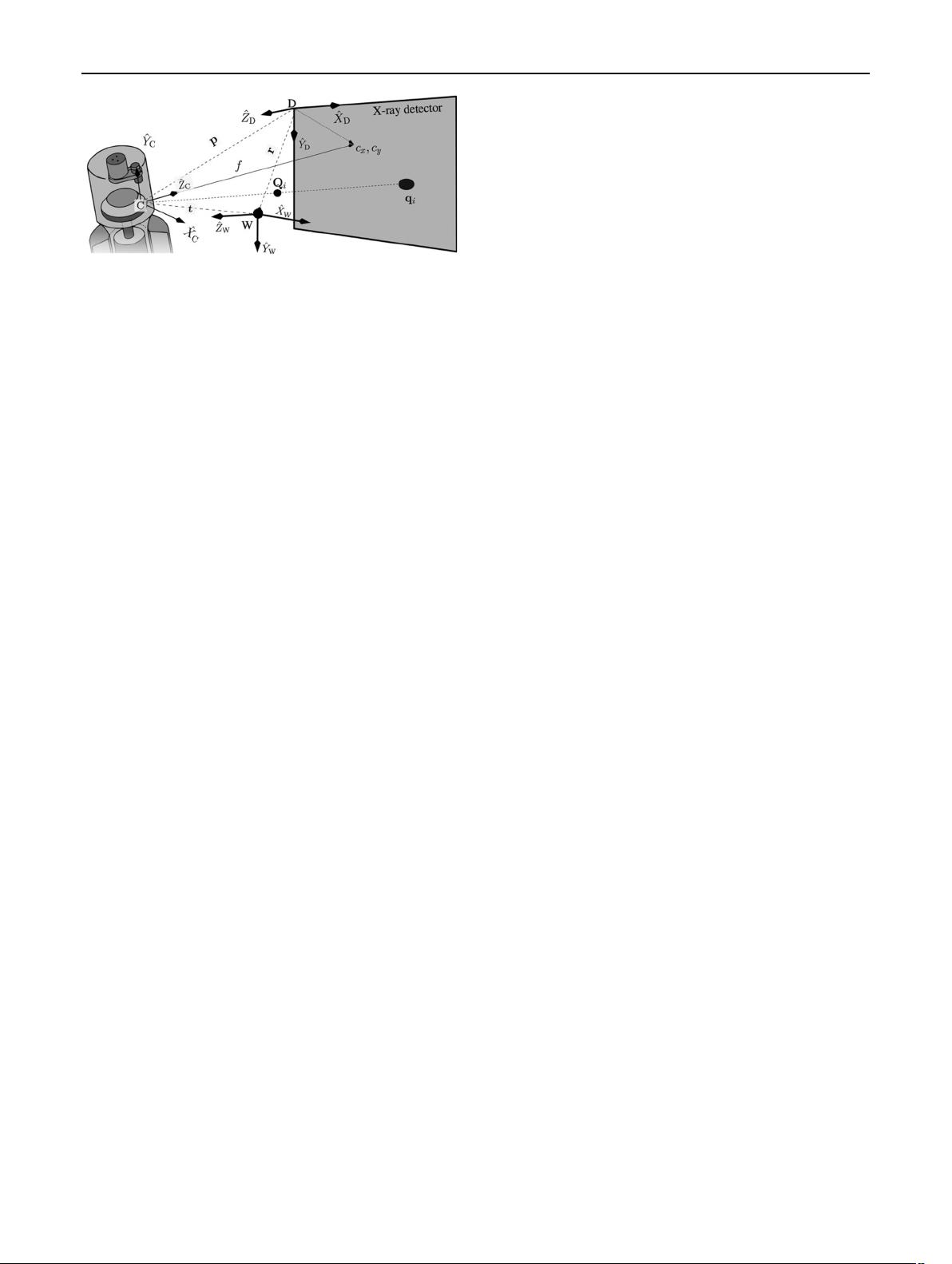
usually placed at a known 3D point in the radiogr aphed
scene, typically, over a frame or DUT. The second one is
the coordinate frame attached to the detect or plate itself,
D ¼
^
X
D
;
^
Y
D
;
^
Z
D
, whose origin is normally coincident
with the upper leftmost pixel. The need to define the
D system originates from the physical fact of working with
a radiation-responsive layer that is not tied to C and from
the possibility of moving the anode and/or detector with
complete freedom around the object in the world coordi-
nate system. Finally, the coordinate system C ¼
^
X
C
;
^
Y
C
;
^
Z
C
has its origin in C itself.
Any point X in the 3D space can be associated with any
of the aforementioned reference frames. For instance, if X
C
represents the coord inates of X relatively to C and X
D
is its
representation relat ively to D, then, from Fig. 2, it can be
verified that:
X
D
¼
10 0
0 10
001
0
@
1
A
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
p rotation about
^
X
C
X
C
þ p ð1Þ
where p = (c
x
, c
y
, f) is known as the principal point and
represents the coordinates of C in D. The line that passes
through C and is perpendicular to the detector plane is the
principal axis and intersects the image plane at the point
(c
x
, c
y
, 0). The distance between C and the detector plane is
the focal length f. The anode C can also be expressed in W
coordinates by means of vector t, which starts at the origin
of W and ends at C.
Finally, if t and p are known, we can derive vector r:
r ¼ p t ð2Þ
which connects the W and D reference frames.
2.3 Camera calibration and projection matrices
As discussed above, a prerequisite for any application in
the field of computer vision is the calibration of the camera.
This step is necessary to determine the pose between the
imaging system and real-world objects. This calibration
involves the calculation of five intrinsic (internal) and six
extrinsic (external) parameters, which can be grouped into
a39 4 matrix, the camera projection/calibration matrix P.
Mathematically, P maps 3D points—expressed in W
coordinates—to 2D points using the expression:
^
q
i
¼ P
^
Q
i
, where each
^
q
i
is an image point and
^
Q
i
is a
W-referenced point, both expressed in homogeneous
coordinates.
As mentioned above, P can be decompos ed into two
blocks of intrinsic (K) and extrinsic parameters. The K
transformation matrix projects 3D points expressed in
terms of the D reference frame to their corresponding
image location on the same reference frame:
K ¼
a
x
sx
0
0 a
y
y
0
001
0
@
1
A
¼
k
x
00
0 k
y
0
001
0
@
1
A
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
k
f r c
x
0 fc
y
00 1
0
@
1
A
ð3Þ
where k is a resolution matrix (described above) expressing
the number of pixels per unit length for both x and y axes,
and a
x
= fk
x
and a
y
= fk
y
represent the focal lengths in
pixel units. Similarly, x
0
and y
0
are the counterparts of c
x
and c
y
in image units. The parameter s is the skewness of
the camera and defines the angle between the x and y axes.
However, as stated above, we assume that pixels are
square, which allows us to simplify Eq. (3) as:
K ¼
a 0 x
0
0 a y
0
00 1
0
@
1
A
ð4Þ
where we have set both focal lengths to be equal to a (this
can generally be assumed in the field of X-ray imaging).
However, this hypothesis should be used with caution in
the case of CR plates, in which the IP scanning process has
its own optical oddities and limitations, as explained by
Rowlands [12] and Dobbins et al. [13].
The extrinsic parameters describe a rigid transformation
that maps points in space between the W and C frames.
This matrix can also be decomposed into a rotation matrix
R (accounting for angles h
x
, h
y
, h
z
) and the translation
vector t described earlier:
½Rjt
zffl}|ffl{
extrinsic matrix
¼ I tðÞ
|fflfflffl{zfflfflffl}
3D translation
R0
01
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
3D rotatio n
zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{
extrinsic matrix
: ð5Þ
A given P can be decomposed into its intrinsic/extrinsic
parts using an RQ decomposition, as suggested by Hartley
[14], because R is orthogonal and K has an upper triangular
shape:
Fig. 2 World (W), detector (D), and anode (C) reference frames. A
Q
i
object is shown in W frame, together with its corresponding
projection q
i
in the D system and relative to the C reference frame
70 F. Albiol et al.









