Python实现LSSVM：最小二乘支持向量机代码及详解

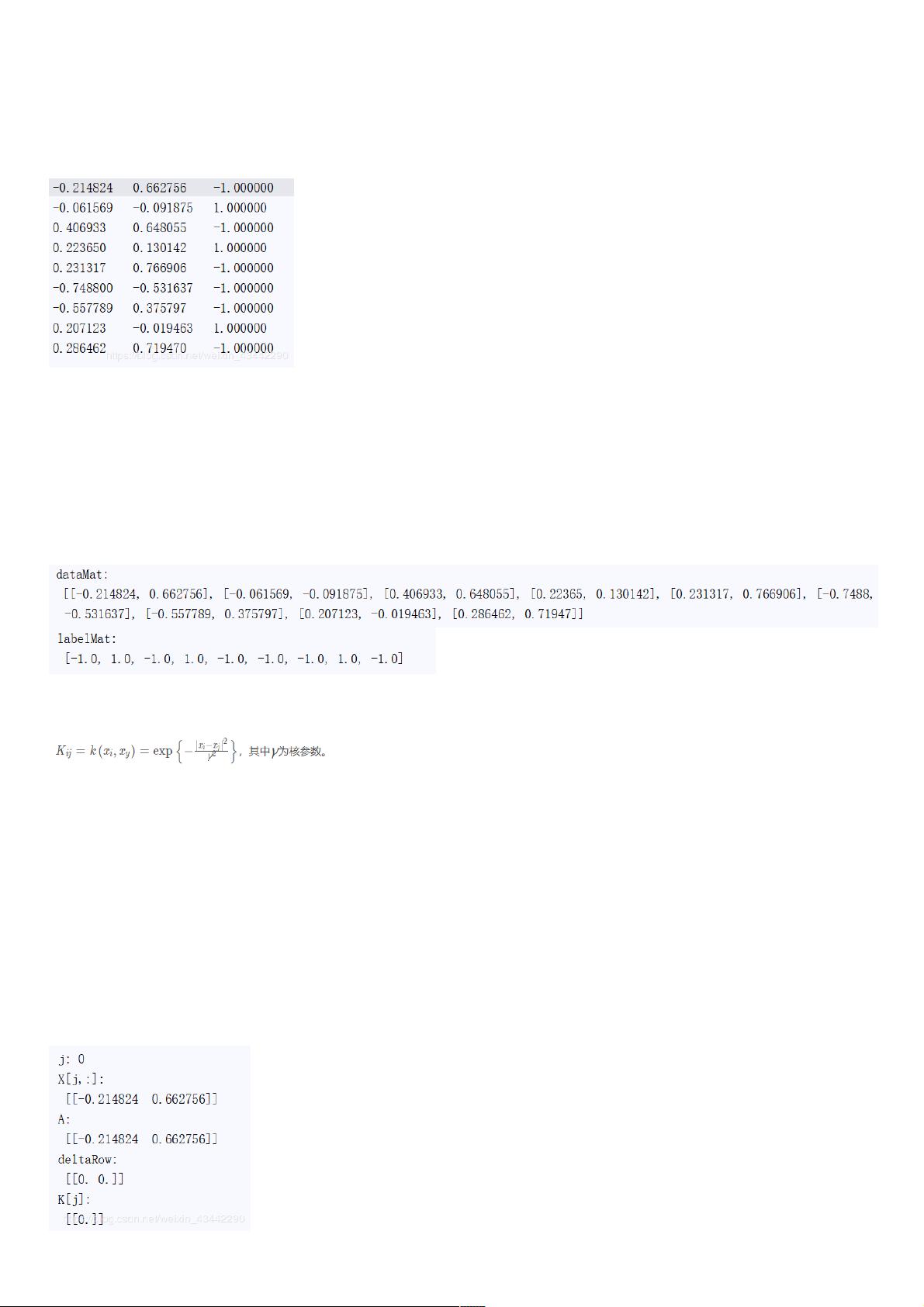
LSSVM (Least Squares Support Vector Machine) 是一种基于支持向量机(SVM)的变种，它通过最小化平方误差而不是最大化间隔来求解分类问题。在Python编程中实现LSSVM的关键在于理解其基本原理、数据预处理和核函数的应用。 首先，我们从导入必要的库开始，`from numpy import *`引入了numpy库，它包含了大量用于数值计算和矩阵操作的功能。数据导入是机器学习的第一步，通过`def loadDataSet(filename)`函数，我们可以读取一个文件中的数据，将样本特征（`dataMat`）和对应的标签（`labelMat`）存储为列表。 接下来，定义核函数是LSSVM的核心部分。核函数的作用是将原始数据从低维空间映射到高维空间，使得原本非线性的数据变得线性可分。在这个例子中，提供了两种常见的核函数：线性核（'lin'）和径向基函数（RBF，'rbf'）。`kernelTrans`函数计算每个数据点与输入向量A的核函数值，对于线性核，只需计算点积；对于RBF，需要计算欧氏距离并应用高斯核公式。 在LSSVM的具体实现中，关键在于`def leastSquares()`方法。这个方法负责求解参数`alphas`和偏置项`b`，它们决定了支持向量在决策边界上的权重和位置。这个过程通常涉及到最小化一个损失函数，该函数结合了模型预测值与真实标签的误差，并考虑了核函数带来的复杂性。通过使用梯度下降或其他优化算法，可以找到使损失函数最小化的参数组合。 在求解参数后，使用`hstack()`函数将特征矩阵与偏置项向量合并成单个矩阵，`vstack()`则用于堆叠多个矩阵。这些函数在构建和操作多维数组时非常有用。最后，还有一个预测主函数，根据训练好的模型对新的输入数据进行分类预测。 LSSVM的Python代码实例展示了如何使用最小二乘法处理支持向量机问题，包括数据加载、特征处理、核函数应用以及参数求解。在实际应用中，理解这些步骤并能够灵活运用到不同数据集上，是实现LSSVM分类能力的关键。