图的广度优先搜索：邻接表实现与C语言描述

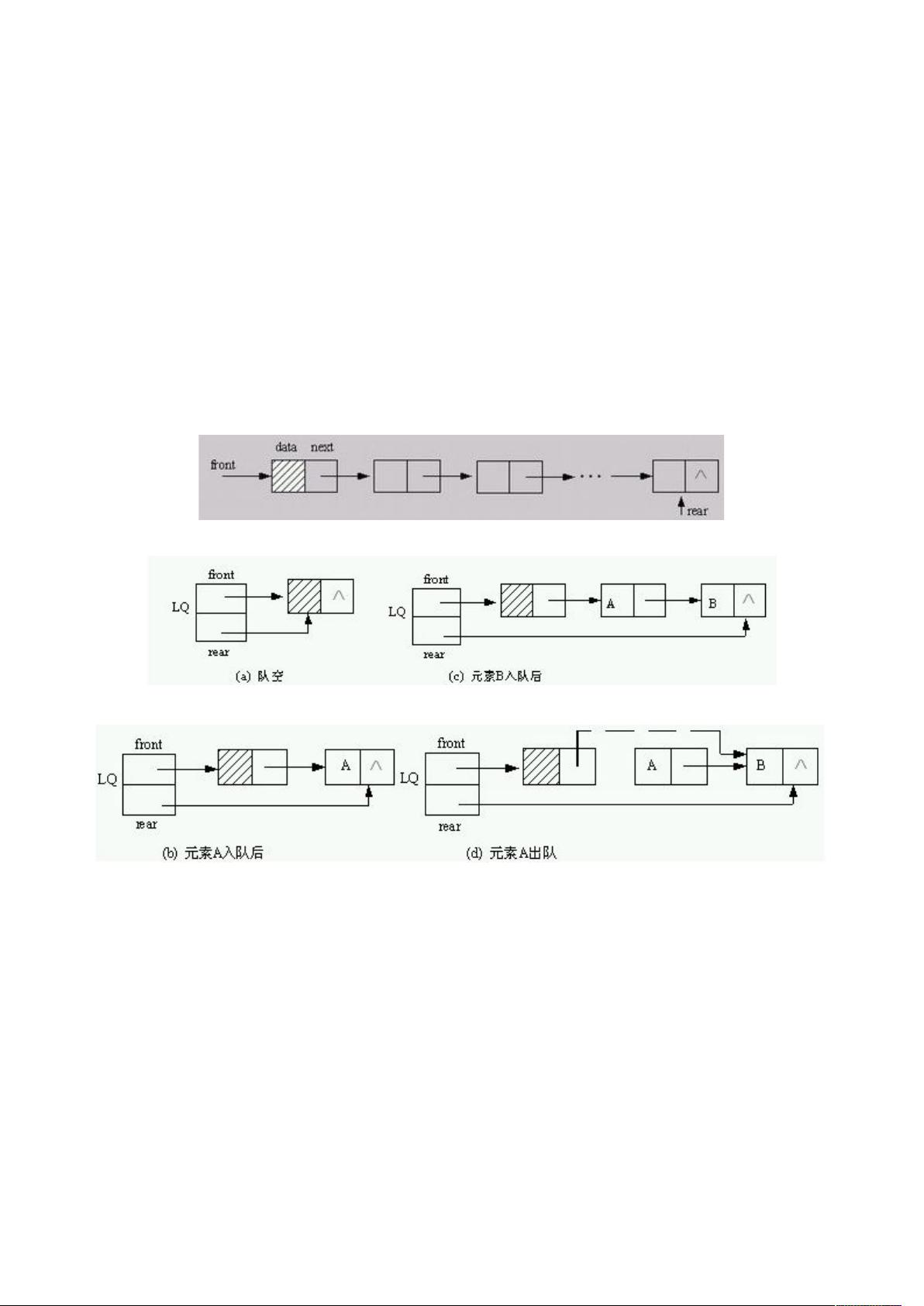
"本文主要介绍了图的广度优先搜索（BFS）算法及其邻接表实现，结合队列数据结构的原理，详细阐述了算法思想和C语言的代码描述。" 在图的遍历中，广度优先搜索（BFS）是一种重要的方法，尤其在处理无向连通图时。该算法的核心思想是从一个起始节点开始，按照层次顺序访问所有可达的节点。在实际操作中，队列作为一种先进先出（FIFO）的数据结构，是实现BFS的关键。 1. **队列**： - **定义**：队列是一种特殊类型的线性表，其中元素的插入发生在队尾，而删除发生在队头，遵循先进先出的原则。 - **链队列实现**：链队列是队列的链式存储结构，包含首指针和尾指针，分别指向链表的头部和尾部。新元素在尾部加入，头部元素被删除，当头指针和尾指针均指向头结点时，表示队列为空。 2. **广度优先搜索算法**： - **算法思想**：BFS类似于树的层次遍历，从选定的初始顶点开始，逐层访问与其相邻的未访问顶点。首先访问初始顶点，然后访问其所有未访问的邻接点，接着访问这些邻接点的未访问邻接点，如此类推，直到遍历完所有顶点。 - **执行步骤**： - 选择一个未访问的顶点作为起点，将其访问标记设为已访问。 - 将该顶点入队。 - 当队列不为空时，取出队首顶点，访问其所有未访问的邻接点，并将这些邻接点入队。 - 重复以上步骤，直到队列为空，即所有顶点都被访问过。 3. **C语言描述的BFS算法**： 在C语言中，BFS可以通过以下步骤实现： - 初始化一个空队列，将起始顶点入队。 - 使用循环来处理队列，每次取出队首顶点，访问它并标记为已访问，然后将它的未访问邻接点入队。 - 循环继续，直到队列为空。 4. **应用**： BFS常用于寻找最短路径、检测连通性、层次遍历等问题，如在社交网络中查找两个用户之间的最短关系路径，或在网络路由中找到两个节点间的最短路径。 总结来说，图的广度优先搜索通过队列数据结构实现，从一个节点出发，按照层次顺序遍历所有节点，是解决许多图论问题的基础算法。在邻接表的表示下，BFS尤其适用于稀疏图，因为它避免了大量不必要的存储空间开销。理解并熟练掌握BFS算法对于理解和解决问题至关重要，特别是在图论和数据结构领域。