"二维随机变量的分布律及边缘分布律；一口袋中球的取球概率问题解析"

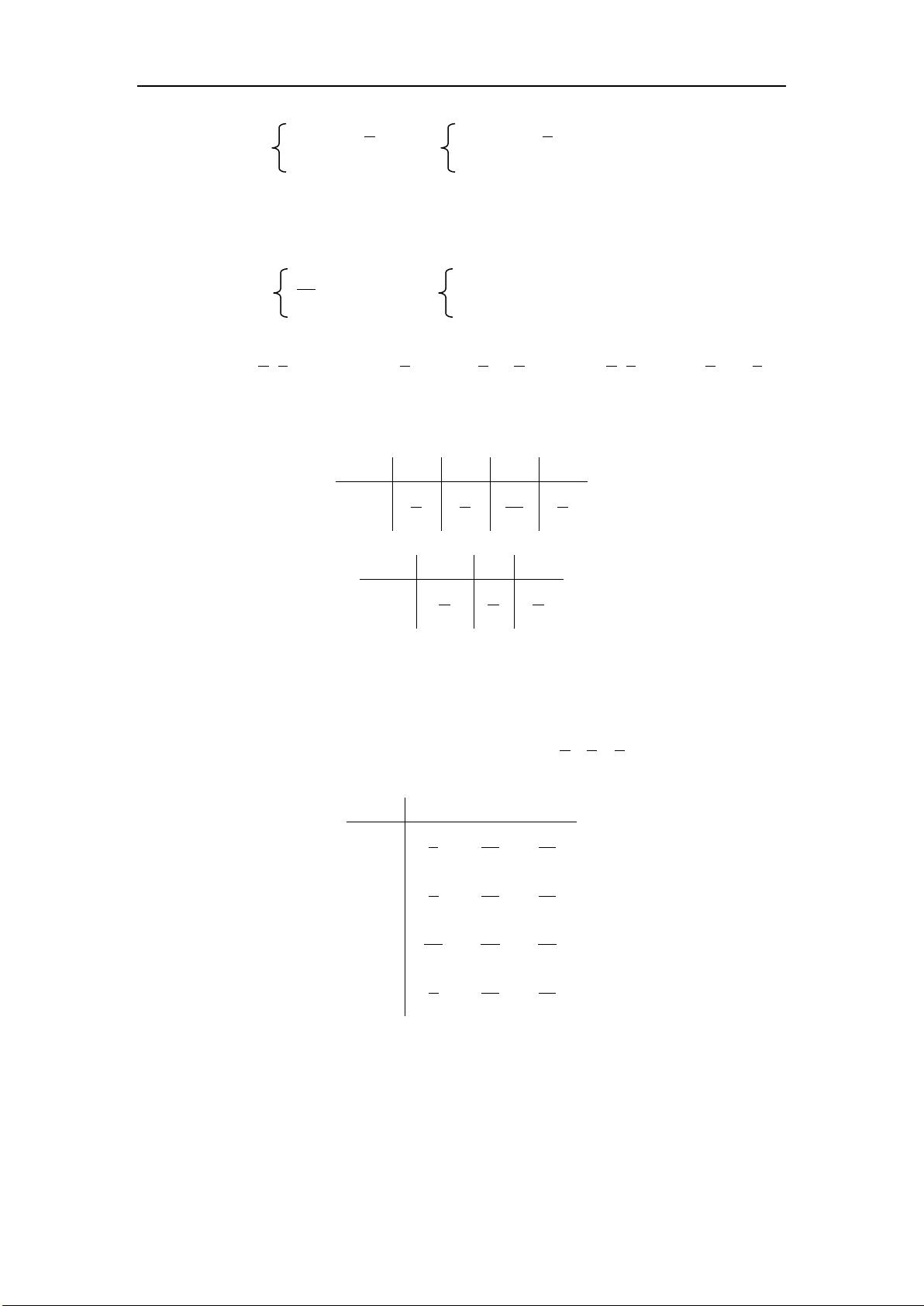
本题包括两个部分： 1. 二维随机变量题目：给出了二维随机变量X和Y只能取特定的数值，以及它们取这些值的概率。根据这些信息，可以求出这二维随机变量的分布律，并分别写出关于X和Y的边缘分布律。通过计算，得到联合分布律为： X\Y 0 3/125 1 1/121 -1 1/31 2 1/61 关于X的边缘分布律为：X=0, P(X=0) = 3/125 + 1/31 = 206/1555 X=1, P(X=1) = 1/121 + 1/61 = 122/3660 X=-1, P(X=-1) = 1/31 X=2, P(X=2) = 1/61 关于Y的边缘分布律为：Y=0, P(Y=0) = 3/125 + 1/61 = 206/3660 Y=1, P(Y=1) = 1/121 + 1/31 = 122/1220 Y=-1, P(Y=-1) = 1/31 2. 取球题目：描述了一口袋中有四个球，标有数字1，2，2，3，且球被取到的可能性相同。根据这些信息，可以求出取球的分布律及两次取球序列的概率。通过计算，得到(Y,X)的分布律为： (Y,X) P(Y,X) (3,3) 1/4 * 1/4 = 1/16 (3,2) 1/4 * 2/4 = 1/8 (3,1) 1/4 * 1/4 = 1/16 (2,3) 2/4 * 1/4 = 1/8 (2,2) 2/4 * 2/4 = 1/4 (2,1) 2/4 * 1/4 = 1/8 (1,3) 1/4 * 1/4 = 1/16 (1,2) 1/4 * 2/4 = 1/8 (1,1) 1/4 * 1/4 = 1/16 在以上计算过程中，我们根据概率的定义和原题给出的具体条件，通过逐步分析并进行概率计算，得出了题目要求的二维随机变量和取球的分布律。这种基于概率论和统计学原理的推导和计算过程，展现了对概率论与数理统计知识点的掌握和应用能力。