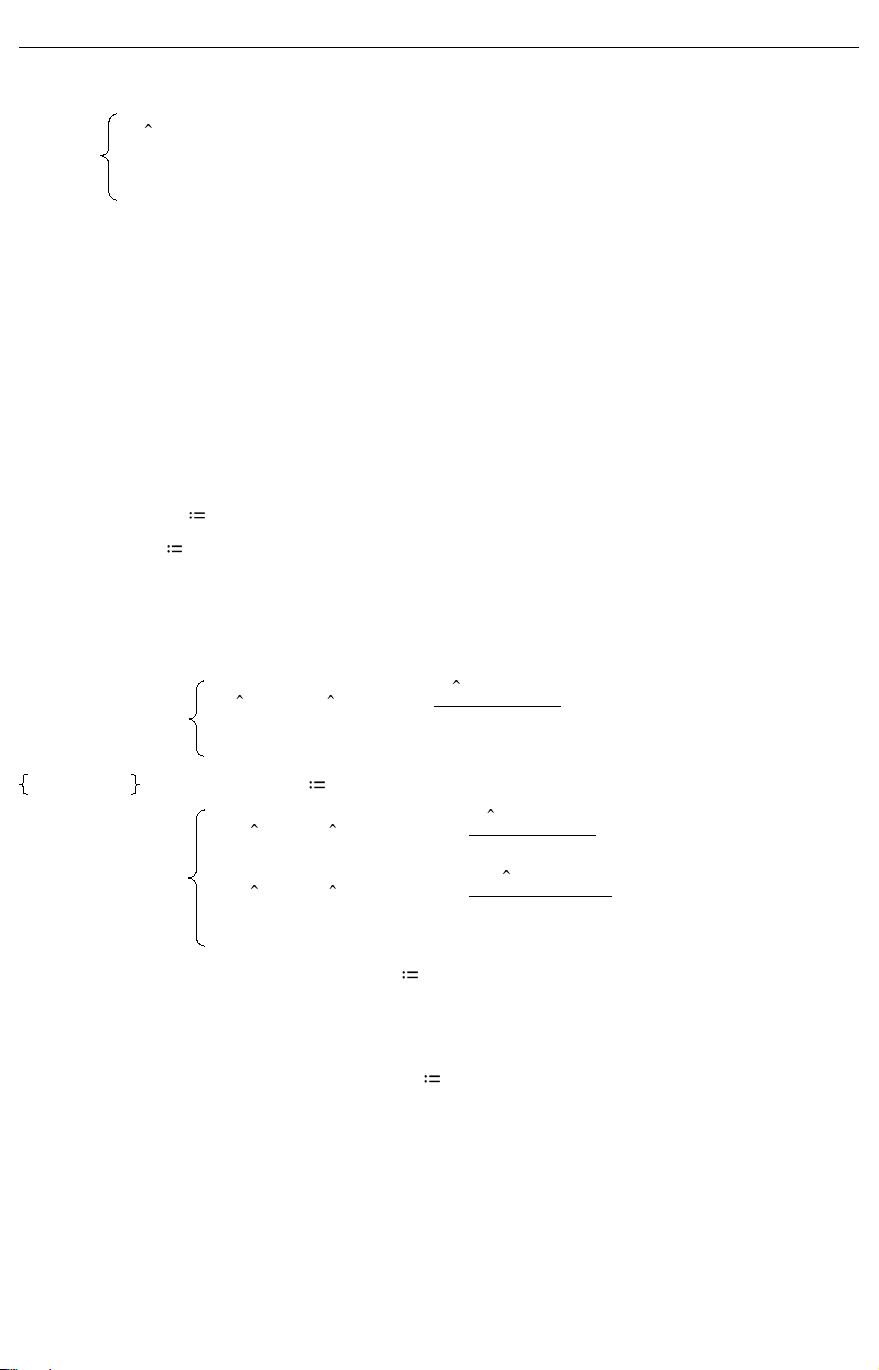多区域拟谱法解非线性对流-扩散方程的稳定性与并行优化

本文主要探讨了非线性对流-扩散方程的多区域拟谱方法，发表于2011年的学术期刊上。该研究针对复杂区域问题，提出了一种创新的数值求解策略。在传统的一维问题中，尽管谱方法在简单区域求解上表现出色，但在处理复杂的几何形状时却面临挑战。多区域方法作为一种解决方案，通过将整个区域划分为多个子区间，每个子区间独立应用谱方法，解决了这个问题。 具体而言，论文的核心内容包括以下几个方面： 1. 方法描述：在每个子区间内，作者采用了Legendre-Galerkin方法作为基础框架，然而对非线性项，特别对待，选择在Legendre/Chebyshev-Gauss-Lobatto点进行处理。这种特殊的配置方式确保了非线性项的精确处理，并利用这些特殊点的特性优化了系数矩阵，使其变得更稀疏，有利于并行计算，从而提高了计算效率。 2. 稳定性与收敛性分析：研究者深入探讨了这种方法的稳定性以及基于L2模的最佳误差估计，这在数值分析中是关键的性能指标，它保证了算法在实际应用中的可靠性和准确性。 3. 多区域与单区域比较：为了验证方法的有效性，文中提供了单区域方法和多区域方法的数值示例，并进行了详细的对比分析，展示了多区域方法在复杂问题上的优越性，如更灵活的分辨率调整、改善的代数方程组条件数以及更好的并行计算潜力。 4. 相关工作背景：论文引用了先前的研究，如Pavoni关于Korteweg-de Vries方程的多区域Chebyshev拟谱方法，以及Quarteroni的线性双曲型方程组多区域配置方法，强调了多区域方法在解决这类问题上的持续发展和应用价值。 这篇文章不仅提供了一种有效的数值求解策略，还对多区域拟谱方法的理论基础和实际应用进行了深入的探讨，为解决非线性对流-扩散方程在复杂区域的计算问题开辟了新的途径。