KMP算法详解与next数组构建深度讲解

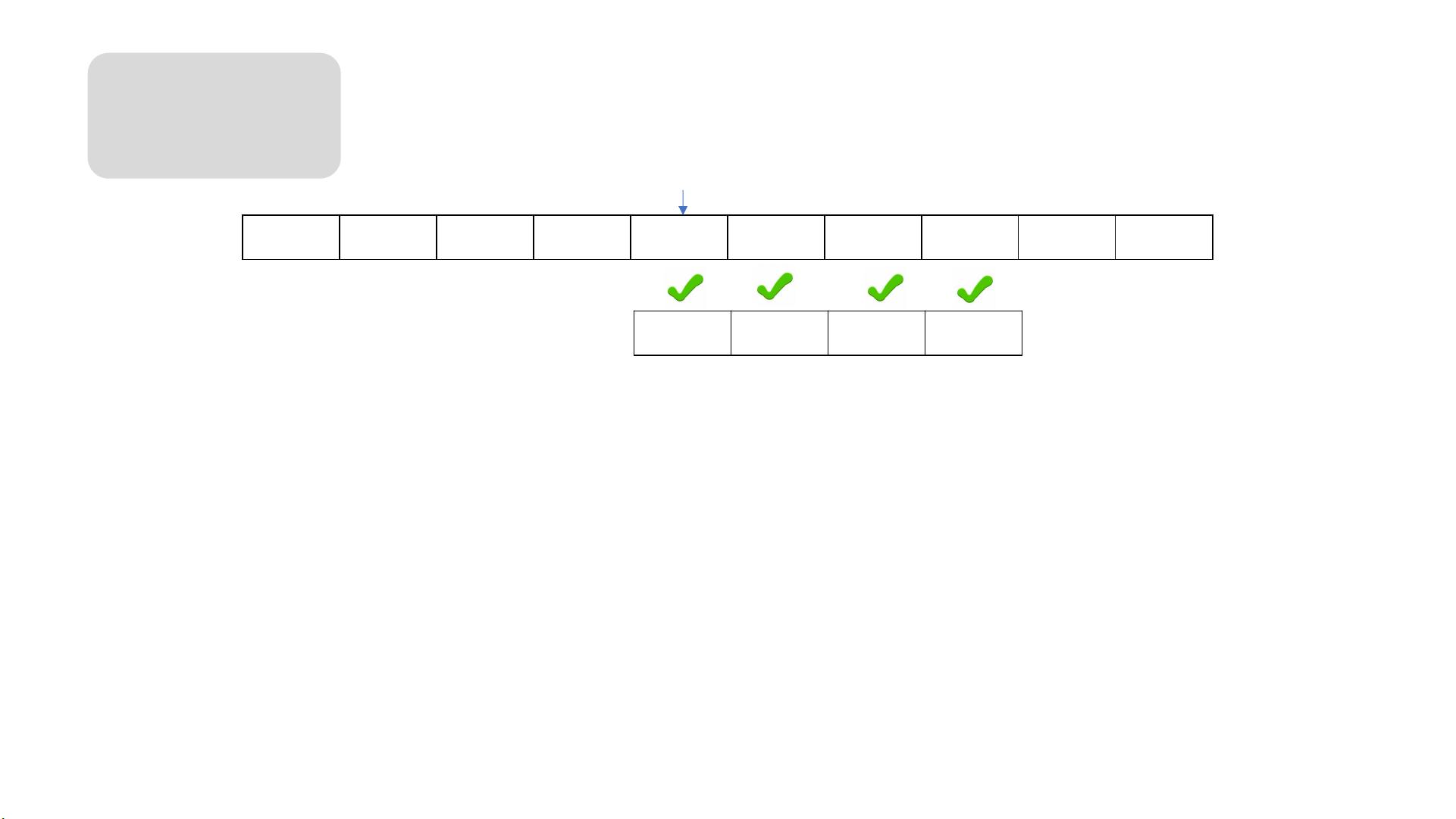
KMP算法是一种高效的字符串匹配算法，由Leslie E. KMP于1977年提出，用于在一个文本串中查找一个模式串。这个算法的核心在于构建一个next数组，用于指导模式串在发生匹配失败时如何高效地跳过已匹配的部分，避免重复搜索。 1. **朴素匹配算法**：这是最基础的字符串匹配方法，逐个字符进行比较，当发现不匹配时就从头开始再次搜索，效率较低，时间复杂度为O(nm)。 2. **KMP算法**：与朴素匹配不同，KMP算法利用next数组优化了搜索过程。next数组存储了模式串中每个位置的“部分匹配失败指针”，它对应于前缀和后缀的最大公共前后缀长度，允许在不匹配时跳过已匹配的字符。这样，即使遇到不匹配，模式串也不再从头开始搜索，而是根据next数组中的值调整位置，减少了无效搜索。 3. **next数组的计算**：通过计算模式串的前缀和后缀集合的交集，确定每个位置的next值。比如在例子中，对于模式串“ababca”，其next数组计算过程显示，当匹配失败时，如从第2个字符开始匹配，next[2] = 1，因为最长的公共前后缀是前一个字符，即“a”。 4. **KMP算法流程**： - 当匹配到i和j位置，若S[i] == P[j]，则i++，j++，继续匹配。 - 若S[i] != P[j]，则根据next[j]的值更新j，跳过已匹配的字符，避免重复搜索。 5. **KMP算法举例**：例如，主字符串“abaacababcac”与模式串“ababca”，当匹配到第2个字符时，由于S[2] != P[2]，根据next[2]=1，模式串会跳过第一个字符，从第三个字符（'a'）继续匹配。 6. **KMP算法的代码实现**：虽然没有直接给出代码，但理解了next数组的构建和使用，可以编写相应的C、Python或其他编程语言的KMP函数，如用C++实现： ```cpp int next[] = {0, 0, 1, 2}; // 假设模式串为"ababca"的next数组 int j = 0; // 当前模式串指针 for (int i = 1; i < main_string.size(); i++) { while (j > 0 && main_string[i] != pattern[j]) { j = next[j - 1]; } if (main_string[i] == pattern[j]) { j++; } if (j == pattern.size()) { // 匹配成功 } } ``` 7. **时间复杂度**：KMP算法显著降低了时间复杂度，一般情况下时间复杂度为O(n + m)，其中n是主字符串长度，m是模式串长度。这是因为每次不匹配时，模式串只向右移动一次或不移动，大大减少了重复搜索。 KMP算法是一种巧妙且高效的字符串匹配策略，通过预处理next数组，能够在最坏情况下达到线性时间复杂度，提高搜索效率。这对于处理大量数据的场景尤其重要。