二维金属圆柱体散射场计算：矩量法MATLAB实现

"基于矩量法的二维金属体散射（内含matlab程序）" 本文主要探讨了如何使用矩量法（Method of Moments, MoM）来计算二维金属圆柱体的散射场，并提供了相应的MATLAB程序。矩量法是一种数值计算方法，常用于电磁场问题的求解，特别是解决复杂形状物体的散射和辐射问题。 1. 问题描述 问题的核心是计算一个二维金属圆柱体在垂直于z轴的TM或TE平面波入射下的散射场。由于金属体的边界条件，其表面电流密度必须为零，这为解决问题提供了基础。 2. 矩量法求解过程 2.1 电场积分方程 首先，基于麦克斯韦方程，建立了电场积分方程，该方程描述了圆柱体表面的面电流如何产生远场。通过对圆柱体表面进行离散化，将连续的积分方程转化为离散方程组。入射场和散射场被定义，然后利用金属表面的边界条件推导出电荷密度与面电流密度的关系。 2.1.2 离散化 通过点匹配法，将圆柱体表面划分为N个部分，每个部分对应一个基函数。基函数选择使得积分方程可以被离散化为一组线性代数方程。 2.1.3 方程组求解 利用LU分解法，可以将离散后的方程组求解为上三角矩阵L和下三角矩阵U的形式，从而求得面电流密度J。有了J，就可以进一步计算散射场E_s和散射截面σ。 2.1.4 结果验证 为了验证计算的准确性，可以通过模式展开法求解同一问题，并比较两者的结果。这确保了所使用的矩量法的正确性和可靠性。 2.2 磁场积分方程 对于TE波入射的情况，只考虑垂直于z轴的磁场分量。利用类似的方法，可以建立磁场积分方程，并同样进行离散化、求解，得到磁场的散射特性。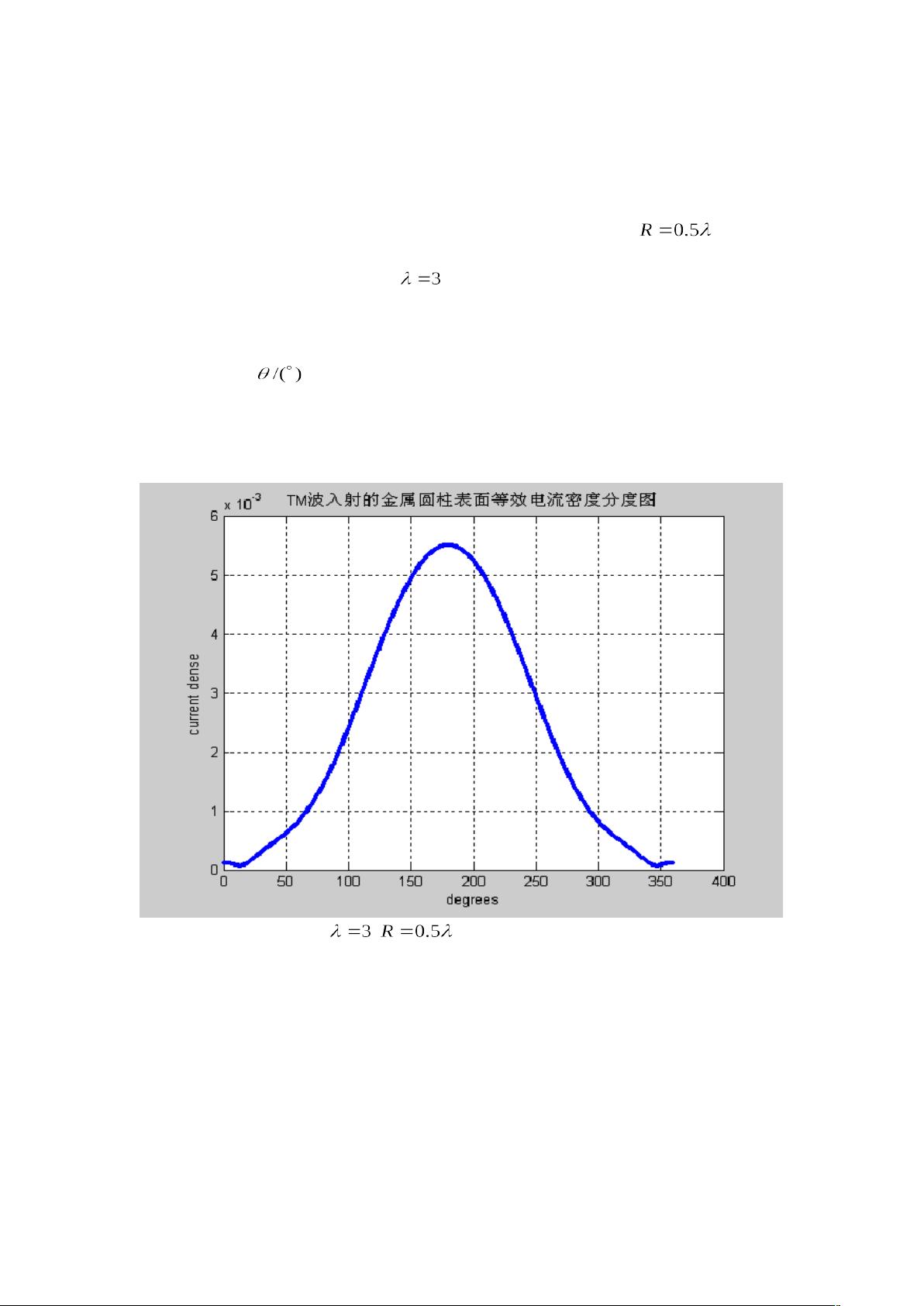 3. 计算机数值实验及分析 这部分通常涉及实际运行MATLAB程序，模拟二维金属圆柱体的散射行为，并分析结果。可能包括散射场的分布、散射截面随频率的变化以及其他相关物理参数的讨论。 这个资源提供了一种使用矩量法求解二维金属圆柱体散射问题的完整流程，包括理论推导、数值方法和验证步骤，并且附带了MATLAB实现，对于理解电磁散射理论和实践计算具有很高的价值。