数学建模实用算法讲义：神经网络、遗传算法等深度解析

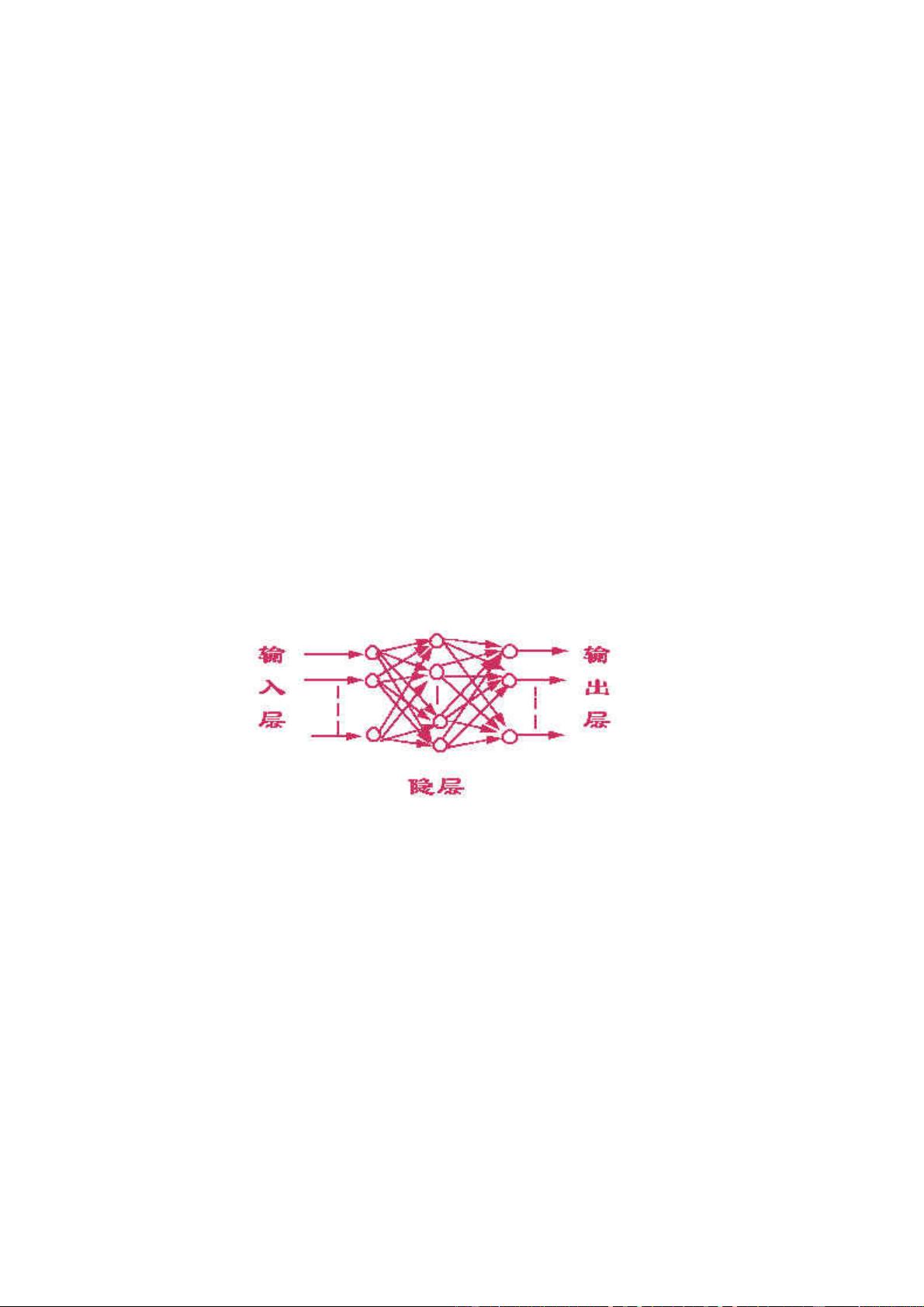
先进C算法讲义深入探讨了数学建模中常用的几种高级算法，如神经网络算法、遗传算法、模拟退火算法和模糊数学方法。这些算法的优势在于它们能够处理常规算法难以解决的复杂问题，尤其是在面对非线性或不确定性的数据时。尽管它们具有深厚的理论基础，但讲义的焦点在于实用应用，而非详尽的理论剖析。 神经网络算法部分，首先介绍了其基本原理，将输入和输出之间的关系视为一个可以训练的"网络"，通过调整节点间的权值，使网络在训练后能根据新的输入预测输出。神经网络由输入层、输出层和可能的隐藏层构成，层数增加可以提高准确性，但计算时间也随之增长。每个节点，即人工神经元，模仿生物神经元工作，具有多个输入、一个输出以及激发函数，不同函数决定了网络的特性和用途。 感知器是最基础的神经网络类型，使用阶跃函数作为神经元的激发函数，主要应用于分类任务。而BP（Backpropagation）网络更为复杂且广泛应用，它通常包含多层结构，使用S型函数如正切或对数函数，功能多样，包括函数逼近、模式识别和分类等。 遗传算法是一种模拟自然选择过程的优化技术，通过模拟生物进化过程，寻找最优解。模拟退火算法则是启发式搜索的一种，通过在一定概率下接受低于当前最佳解的解，有助于跳出局部最优，找到全局最优。 模糊数学方法利用模糊逻辑处理不确定性，允许系统在一定程度上处理模糊的输入和输出，适合于处理模糊领域的问题。 讲义提供了相关的程序代码示例，让学习者可以直接应用这些算法来解决实际的数学建模问题，而不必深入研究每种算法的理论细节。通过本讲义的学习，读者应能掌握这些算法的大致原理，了解它们在数学建模中的应用场景，并能有效地运用到实际问题中。