FPGA实现幅度调制连续波超声测距器的重构相锁定方案研究
需积分: 3 179 浏览量
更新于2024-09-10
收藏 1.37MB PDF 举报
本文档探讨了在FPGA中实现一种幅度调制连续波（AMCW）超声测距器的方法，利用了重构相锁定环（RPLL）与滑动离散傅里叶变换（SDFT）。该技术基于最近提出的集成相位锁定方案，旨在提高超声测距系统的精度和性能。
首先，文章介绍了一种创新的系统架构，通过结合SDFT和RPLL，能够实时分析和解调超声信号中的频率成分。传统的相锁定环用于保持本地振荡器的频率与接收信号同步，而重构策略允许更灵活和高效地处理信号，尤其是在高数据率下，这在实时测距应用中至关重要。
SDFT在此处的作用是将连续的超声波信号分解成一系列离散频谱，这有助于减少噪声影响，同时提供了关于信号强度和频率变化的宝贵信息。通过滑动窗口技术，SDFT能够捕捉信号随时间的变化，从而实现动态范围的扩展和精确的距离测量。
RPLL的重构则涉及对传统设计的优化，可能包括改进的锁相环路滤波器、采样率调整、以及更高效的算法实现。这种优化有助于减小功耗、降低复杂度，并且可能提升了系统对噪声和干扰的抗扰能力。
论文作者Sumathi和Janakiraman来自DA-IICT和印度理工学院马德拉斯分校，他们分别来自信息通信技术和电气工程领域，强调了这项工作的学术贡献和合作背景。他们的研究着重于提供一个开源的文章，遵循Creative Commons Attribution License，允许广泛的使用、分发和复制，只要原始作品得到适当的引用。
这篇论文提供了一个创新的FPGA实现方案，针对幅度调制连续波超声测距技术，通过重构的相锁定环路和滑动离散傅里叶变换，展示了如何提升测距系统的性能，对于电子工程师、信号处理专家以及超声传感器开发者来说，具有重要的参考价值。
VLSI Design 3
(Periodic signal)
Input
ena0
NCO
f
s
Sampling
pulses
Limiter
ena0
= 25.6kHz
PI controller
ena0
Moving
averager
ena
ena
Counter
Address
LUT
Cos
Cosine
Sine
SDFT
ena
Phase
detector
×
+
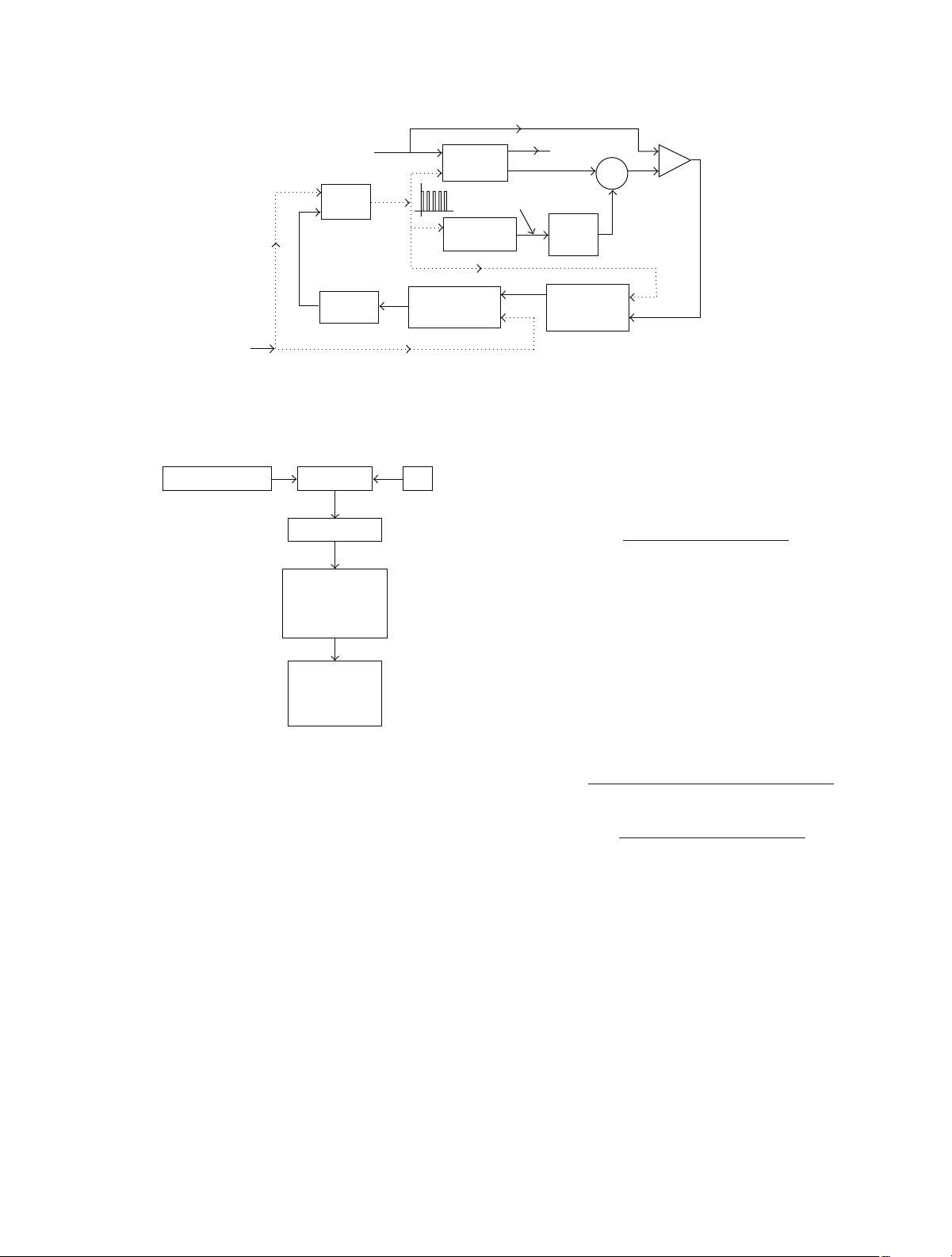
Figure 2: Block diagram of restructured phase-locking scheme.
MATLAB/Simulink DSP builder
IP
Signal compiler
Ve r i l o g o r V H DL
.Tcl files to run
synthesis,
place, and route
Synthesis and
Quartus-II
software place
and route
Design in
MATLAB
/Simulink
Convert to
FPGA design
System verification
and construction
Figure 3: Synthesis flow of Matlab/Simulink-DSP builder and
Quartus-II.
signal from the LUT reduces the steady residual error present
in the control signal of the NCO [13]. The modification
results in the NCO output frequency becoming very accurate
compared to the simple integrated phase-locking scheme
(IPLL), and hence provides fine phase locking with the
fundamental component of the input signal.
2.1. DSP Builder-Quartus-II Tool. The MATLAB/Simulink-
DSP builder software had been used for realizing the
proposed Sliding DFT-based RPLL scheme. DSP Builder
signal compiler block reads Simulink model files (.mdl)
which are built using DSP builder and MegaCore blocks and
generates VHDL files and Tool command languages (.Tcl)
scripts for synthesis [14], hardware implementation, and
simulation. The synthesis flow of the DSP builder tool and
Quartus-II to generate the VHDL codes is shown in Figure 3.
The generated VHDL codes can be downloaded into FPGA
from PC through JTAG cable for processing.
2.2. Sliding DFT. The SDFT transfer function including the
damping factor “r” can be expressed as
H
k
(
z
)
=
1 − r
N
z
−N
z
−1
re
j2πk/N
1 − re
j2πk/N
z
−1
,
r<1,
[
k
= 0, 1, 2, 3, ..., N − 1
]
,
(1)
where k is the bin index, which can vary from 0 to N
− 1,
and N is the window width. The damping factor r<1
is introduced in the SDFT transfer function [15]toavoid
numerical instability. The in-phase and quadrature signals
can be obtained from SDFT block. For k
= 1, the SDFT can
extract the fundamental component present in the received
signal. The real and imaginary parts of the SDFT transfer
function can be written as
Re
[
H
1
(
z
)
]
=
1 − r
N
z
−N
z
−1
r cos
(
2π/N
)
− r
2
z
−1
1 − 2r cos
(
2π/N
)
z
−1
+ r
2
z
−2
,
Im
[
H
1
(
z
)
]
=
1 − r
N
z
−N
z
−1
(
r sin
(
2π/N
))
1 − 2r cos
(
2π/N
)
z
−1
+ r
2
z
−2
.
(2)
The block diagram realization of the SDFT transfer function
giveninequationin(1) is shown in Figure 4(a).Acomb
filter and a resonator are connected in cascade in the
SDFT structure. For the sake of clarity, bus-width and port
symbols were removed in the realization diagram shown in
Figure 4(a). The SDFT transfer function has N number of
zeros and a single pole lying on the unit circle in the z-
plane. For k
= 1, the single pole at z = e
j2π/N
cancels the
zero corresponding to that location. The SDFT is a tuned
filter, which passes only fundamental frequency present in
the input signal and rejects all other harmonics and d.c.
The pole-zero diagram of the SDFT is shown in Figure 4(b).
The damping factor r is chosen as 0.9997. For maintaining
the accuracy, a floating-point bit format of [2 : 18] (bus
width) has been used for the variables in the SDFT block.
The magnitude of the input signal is chosen small enough to
avoid over-flow.
剩余10页未读，继续阅读
点击了解资源详情
点击了解资源详情
329 浏览量
2020-02-24 上传
2021-02-13 上传
2021-02-06 上传
2021-02-07 上传
2021-02-05 上传
2021-02-05 上传
137 浏览量
mahao007
- 粉丝: 7
- 资源: 20
我的内容管理
展开
