BP算法详解与Python实现

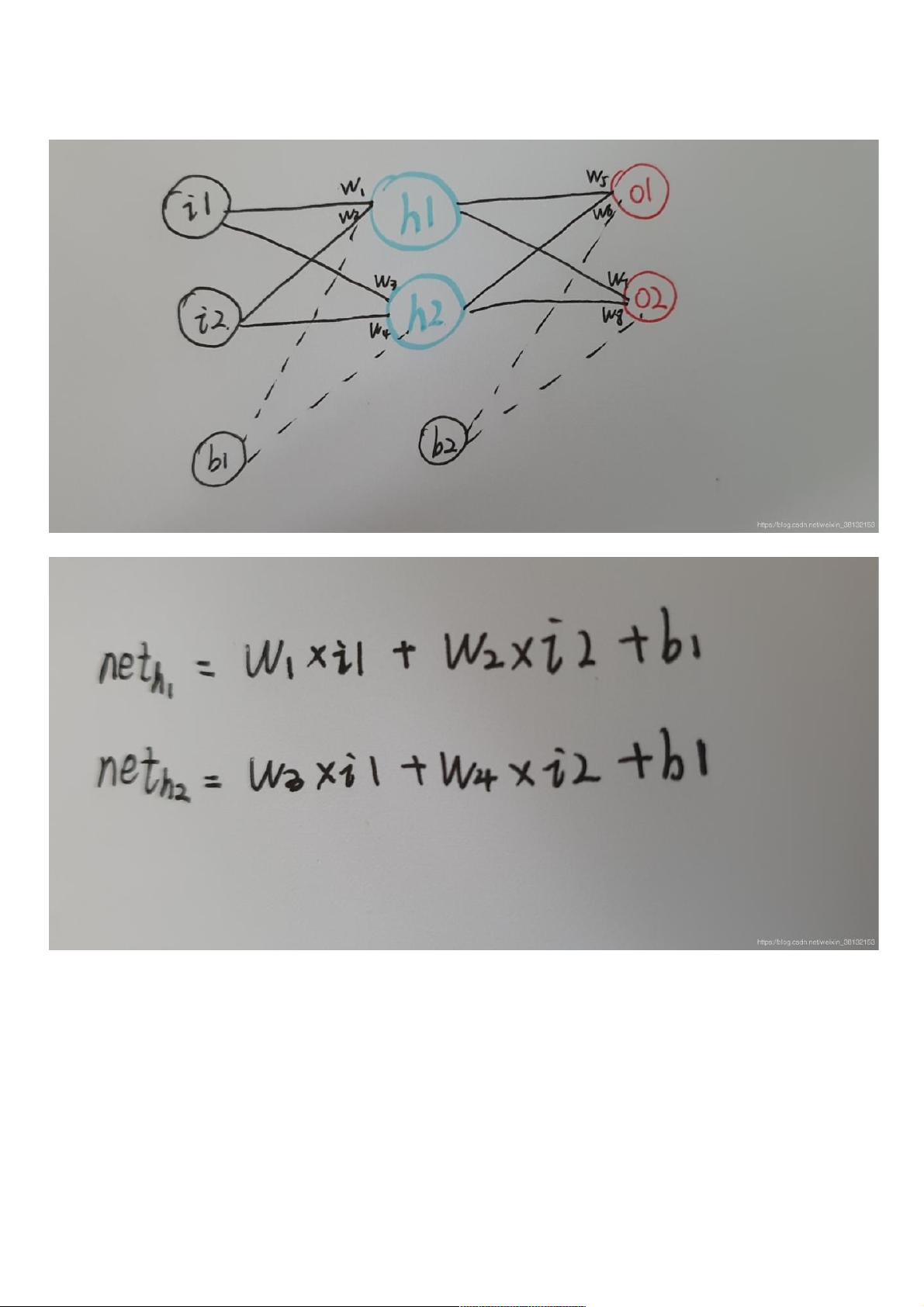
"手推BP算法及python实现" BP算法，全称为Backpropagation（反向传播）算法，是一种在多层神经网络中进行权重更新的常用方法，用于训练神经网络模型。该算法结合了梯度下降法，通过计算损失函数相对于每个权重的梯度，自反向传播误差，从而更新网络中的权重，逐步减小预测结果与实际目标之间的差距。 在正向传播阶段，数据从输入层经过隐藏层（若有的话）传递到输出层。在每个神经元中，输入值与权重相乘后加上偏置，然后通过激活函数（例如Sigmoid函数）转换为非线性输出。Sigmoid函数的表达式为：\( f(x) = \frac{1}{1 + e^{-x}} \)，它将任意实数值映射到 (0, 1) 范围内，有助于引入非线性特性。 对于一个简单的神经网络，正向传播过程如下： 1. 输入层到隐藏层：输入值乘以输入层到隐藏层的权重，加上偏置，然后通过Sigmoid激活。 2. 隐藏层到输出层：隐藏层的输出乘以隐藏层到输出层的权重，加上偏置，再次通过Sigmoid激活，得到最终的输出值。 在反向传播阶段，计算网络输出与目标值之间的误差，然后根据误差反向更新权重。主要步骤包括： 1. 计算输出层误差：误差等于期望输出与实际输出之差。 2. 输出层到隐藏层的权重更新：如以w5为例，计算w5对总误差的贡献，即w5的梯度，然后用学习率(lr)乘以梯度来更新w5。 3. 隐藏层到输入层的权重更新：类似地，计算所有隐藏层到输入层权重的梯度并进行更新。 在实际的Python实现中，通常会使用NumPy库来处理矩阵运算，提高效率。以下是一个简单的BP算法Python代码片段： ```python import numpy as np def sigmoid(x): return 1 / (1 + np.exp(-x)) # 初始化参数 lr = 0.05 # 学习率 Iter = 100001 # 迭代次数 w1 = [[0.10, 0.20], [0.30, 0.40]] # 输入层到隐藏层权值 w2 = [[0.50, 0.60], [0.70, 0.80]] # 隐藏层到输出层权值 b1 = 0.10 # bias b2 = 0.20 input = [0.05, 0.10] # 输入 target = [0.50, 1.00] # 输出 # BP算法迭代 for _ in range(Iter): # 正向传播 net1 = np.dot(w1, input) + b1 net_out = sigmoid(net1) net2 = np.dot(w2, net_out) + b2 out = sigmoid(net2) # 反向传播 delta2 = np.multiply(-(target - out), np.multiply(out, 1 - out)) * net_out delta1 = np.multiply(np.dot(np.array(w2).T, delta2), np.multiply(net_out, 1 - net_out)) * np.array(input) # 权重更新 for i in range(len(w1)): # 更新w1 for j in range(len(w1[0])): w1[i][j] -= lr * delta1[i] * input[j] for i in range(len(w2)): # 更新w2 for j in range(len(w2[0])): w2[i][j] -= lr * delta2[i] * net_out[j] ``` 这段代码实现了BP算法的基本流程，包括正向传播计算输出，反向传播计算误差和更新权重，以及在多个迭代周期内的整个训练过程。注意，实际应用中可能需要加入更多的优化措施，比如动量法、学习率衰减等，以提高训练效果和防止过拟合。