Jðc
k
Þ¼
X
x
i
2c
k
jjx
i
l
k
jj
2
:
The goal of K-means is to minimize the sum of the squared error
over all K clusters,
JðCÞ¼
X
K
k¼1
X
x
i
2c
k
jjx
i
l
k
jj
2
:
Minimizing this objective function is known to be an NP-hard prob-
lem (even for K =2)(Drineas et al., 1999). Thus K-means, which is a
greedy algorithm, can only converge to a local minimum, even
though recent study has shown with a large probability K-means
could converge to the global optimum when clusters are well sep-
arated (Meila, 2006). K-means starts with an initial partition with
K clusters and assign patterns to clusters so as to reduce the squared
error. Since the squared error always decreases with an increase in
the number of clusters K (with J(C)=0 when K = n), it can be mini-
mized only for a fixed number of clusters. The main steps of K-
means algorithm are as follows (Jain and Dubes, 1988):
1. Select an initial partition with K clusters; repeat steps 2 and 3
until cluster membership stabilizes.
2. Generate a new partition by assigning each pattern to its closest
cluster center.
3. Compute new cluster centers.
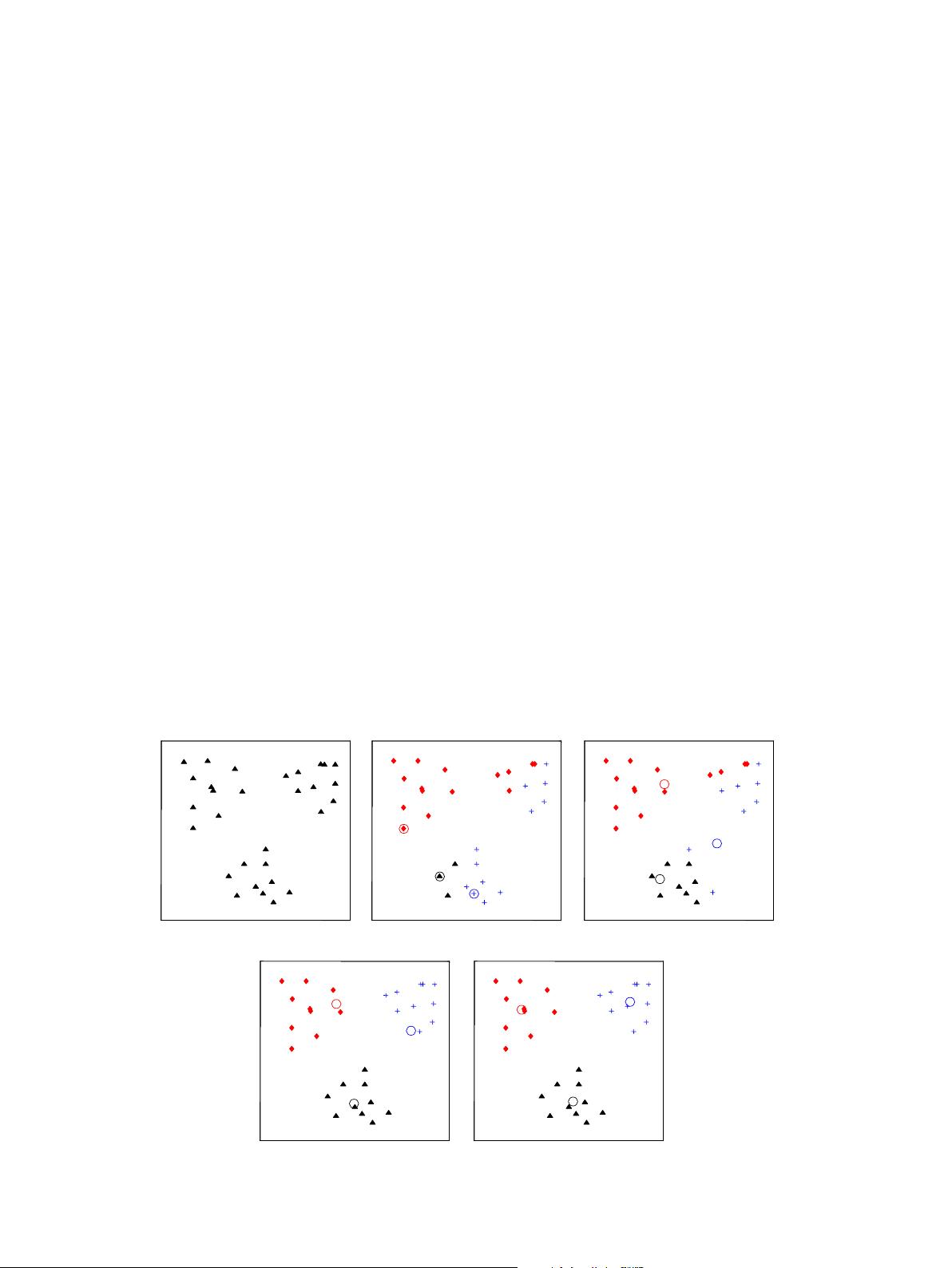
Fig. 4 shows an illustration of the K-means algorithm on a 2-
dimensional dataset with three clusters.
2.4. Parameters of K-means
The K-means algorithm requires three user-specified parame-
ters: number of clusters K, cluster initialization, and distance met-
ric. The most critical choice is K. While no perfect mathematical
criterion exists, a number of heuristics (see (Tibshirani et al.,
2001), and discussion therein) are available for choosing K. Typi-
cally, K-means is run independently for different values of K and
the partition that appears the most meaningful to the domain ex-
pert is selected. Different initializations can lead to different final
clustering because K-means only converges to local minima. One
way to overcome the local minima is to run the K-means algo-
rithm, for a given K, with multiple different initial partitions and
choose the partition with the smallest squared error.
K-means is typically used with the Euclidean metric for com-
puting the distance between points and cluster centers. As a result,
K-means finds spherical or ball-shaped clusters in data. K-means
with Mahalanobis distance metric has been used to detect hyper-
ellipsoidal clusters (Mao and Jain, 1996), but this comes at the ex-
pense of higher computational cost. A variant of K-means using the
Itakura–Saito distance has been used for vector quantization in
speech processing (Linde et al., 1980) and K-means with L
1
dis-
tance was proposed in (Kashima et al., 2008). Banerjee et al.
(2004) exploits the family of Bregman distances for K-means.
2.5. Extensions of K-means
The basic K-means algorithm has been extended in many differ-
ent ways. Some of these extensions deal with additional heuristics
involving the minimum cluster size and merging and splitting clus-
ters. Two well-known variants of K-means in pattern recognition
literature are ISODATA Ball and Hall (1965) and FORGY Forgy
(1965). In K-means, each data point is assigned to a single cluster
(called hard assignment). Fuzzy c-means, proposed by Dunn
(1973) and later improved by Bezdek (1981), is an extension of
K-means where each data point can be a member of multiple clus-
ters with a membership value (soft assignment). A good overview of
fuzzy set based clustering is available in (Backer, 1978). Data
reduction by replacing group examples with their centroids before
clustering them was used to speed up K-means and fuzzy C-means
in (Eschrich et al., 2003). Some of the other significant modifica-
(a) Input data (b) Seed point selection (c) Iteration 2
(d) Iteration 3 (e) Final clustering
Fig. 4. Illustration of K-means algorithm. (a) Two-dimensional input data with three clusters; (b) three seed points selected as cluster centers and initial assignment of the
data points to clusters; (c) and (d) intermediate iterations updating cluster labels and their centers; (e) final clustering obtained by K-means algorithm at convergence.
654 A.K. Jain / Pattern Recognition Letters 31 (2010) 651–666









