支持向量机(SVM)基础解析

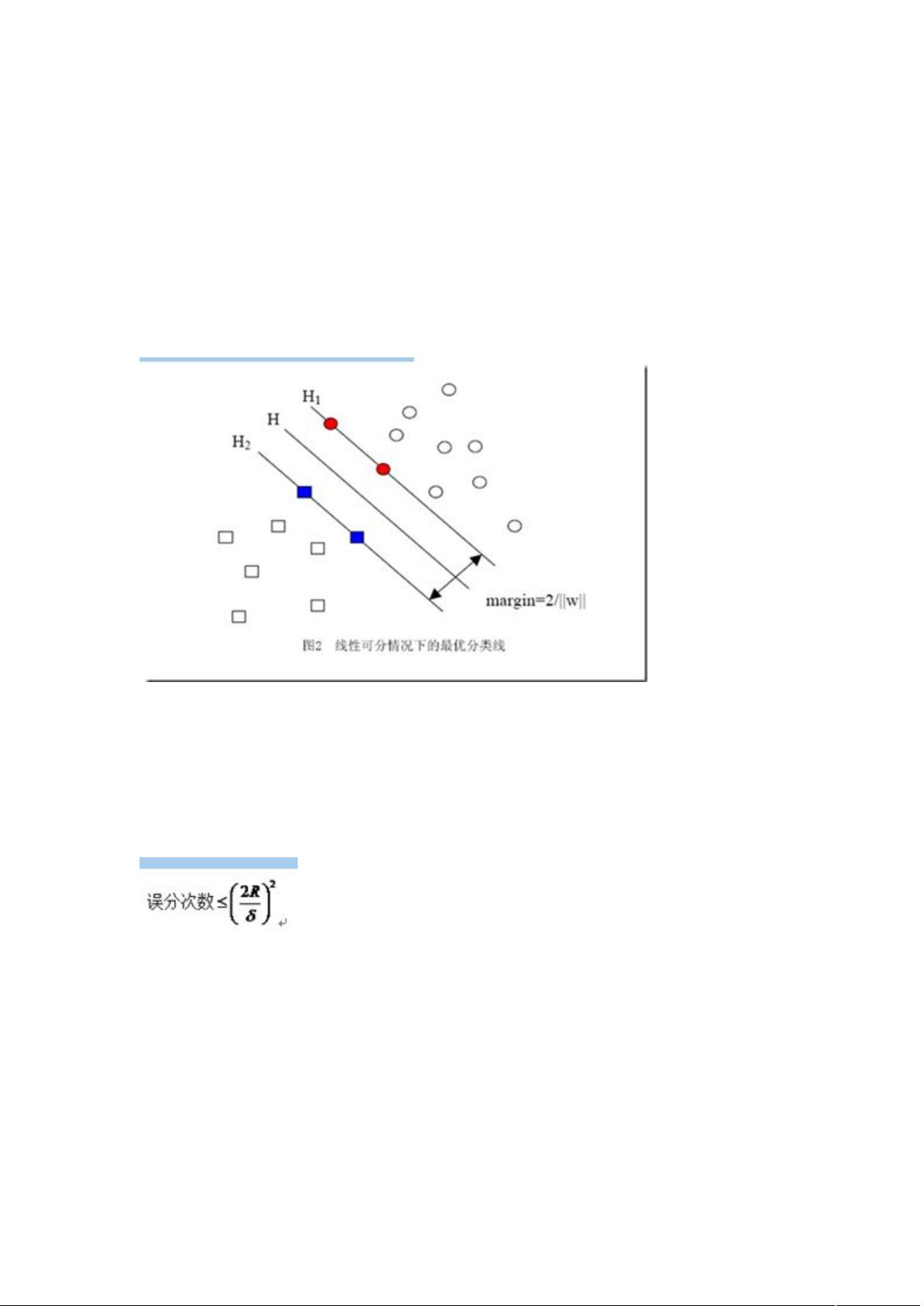
"SVM入门讲解" 支持向量机（Support Vector Machine，SVM）是一种强大的监督学习算法，尤其适用于小样本、非线性和高维数据的分类与回归任务。SVM的核心思想是找到一个最优超平面，使得不同类别的样本被最大化地分隔开。在1995年，Cortes和Vapnik首次提出了SVM的概念，它基于统计学习理论的VC维理论和结构风险最小化原则。 VC维（Vapnik-Chervonenkis Dimension）是衡量一个模型复杂度的重要指标，它表示一个模型能够完美分类的最多样本数。高VC维意味着模型更复杂，可能过拟合；低VC维则可能导致模型过于简单，欠拟合。SVM的独特之处在于它寻找的是具有最小结构风险的模型，即在保证分类性能的同时尽可能降低过拟合的风险。 结构风险最小化是指在训练过程中，不仅要考虑模型在现有样本上的表现（经验风险），还要考虑到未来未知样本的泛化能力（即推广能力）。SVM通过在训练集上找到一个分类边界，同时最大化边界两侧的间隔，从而实现对未知样本的最优预测。这种方法避免了过于依赖训练数据，提高了模型的稳定性和泛化能力。 在SVM中，核函数是一个关键概念，它允许我们将数据从原始特征空间映射到高维空间，以便在高维空间中找到线性可分的超平面。常见的核函数有线性核、多项式核、高斯核（RBF）等。例如，高斯核可以将低维线性不可分的数据转化为高维线性可分，从而解决非线性问题。 SVM的一个显著优点是它的鲁棒性，即使在高维特征空间中，由于采用核函数，计算复杂度依然相对较低，这是传统方法难以比拟的。因此，SVM在处理如文本分类、图像识别等领域表现出色。 SVM通过优化分类边界，寻找最大间隔的超平面，结合统计学习理论的VC维和结构风险最小化，提供了一种高效且泛化能力强的机器学习工具。对于初学者来说，理解这些基本概念以及如何选择合适的核函数是掌握SVM的关键。通过不断实践和理论学习，我们可以更好地运用SVM解决实际问题。