普林斯顿公开课：红黑树详解与平衡搜索树算法

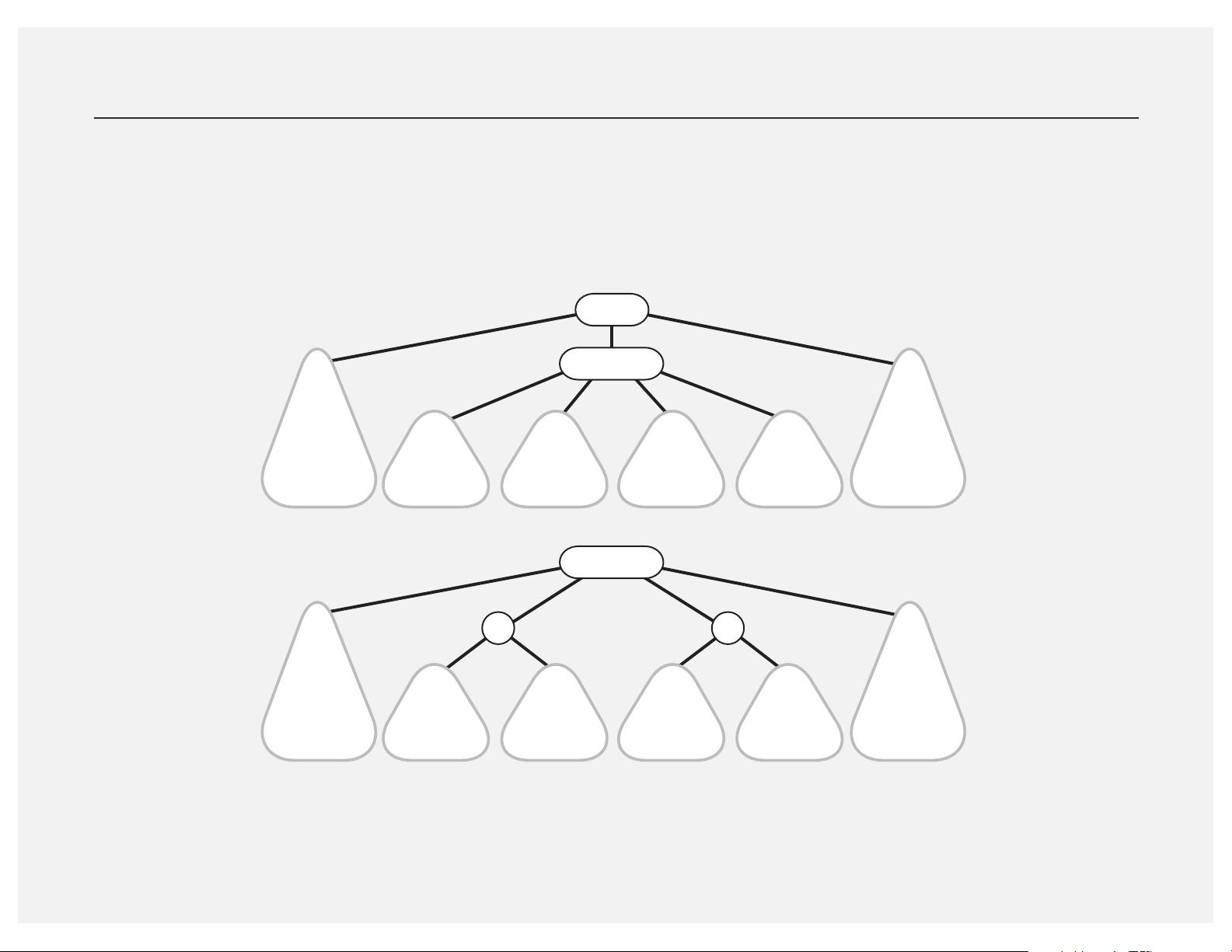
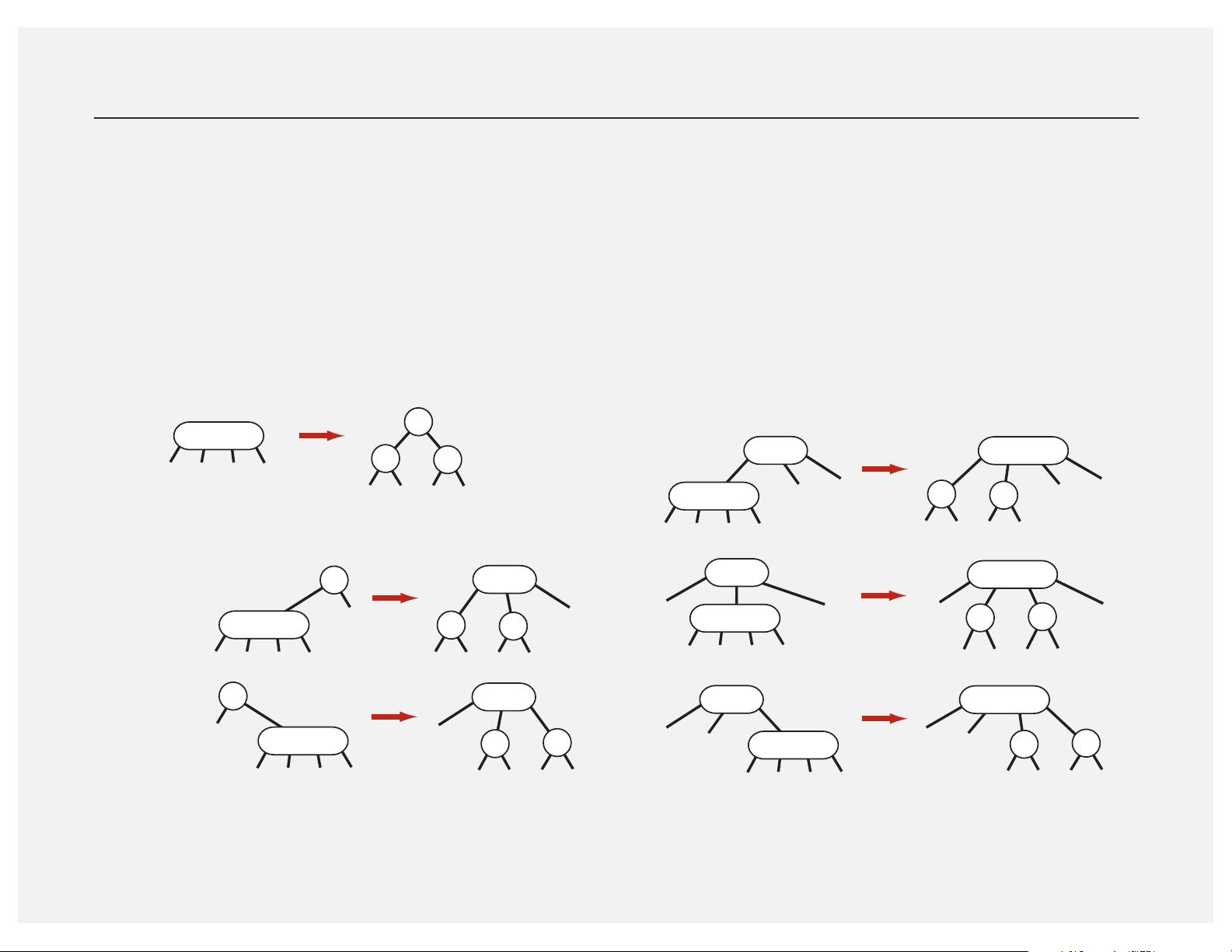
平衡搜索树是数据结构中的一个重要概念，它在算法设计中扮演着关键角色，尤其是在保证高效查找、插入和删除操作的同时维持良好的性能。在这份来自普林斯顿大学算法公开课的详细讲解材料中，主要讨论了三种常见的平衡搜索树：2-3搜索树、红黑树（Red-Black BST）和B树。 首先，2-3搜索树是一种简单的平衡搜索树，每个节点最多包含两个键值，其中一个是根键，另外两个键分别对应两个子节点。这种设计允许在每个层次上保持较小的不平衡，从而减少查找时间。然而，2-3搜索树可能会导致高度不均匀，因此不是最高效的平衡方法。 接下来，红黑树（Red-Black Tree）是一种更为成熟且广泛应用的平衡搜索树，由罗伯特·希拉德和伦道夫·尼尔森于1978年提出。红黑树通过颜色标记节点来确保其平衡性，每个节点被标记为红色或黑色。它规定了一些基本性质，如根节点始终为黑色，任何叶子节点（空节点）都是黑色，以及从任意节点到其每个叶子的所有路径都包含相同数量的黑色节点。这些规则保证了红黑树的高度最多比理想情况下的二叉搜索树高出一倍，即平均查找时间复杂度为O(log N)。此外，插入和删除操作后，红黑树会通过旋转和颜色调整保持平衡，这使得红黑树成为许多实际应用的理想选择，如C++标准库中的`std::map`和`std::set`。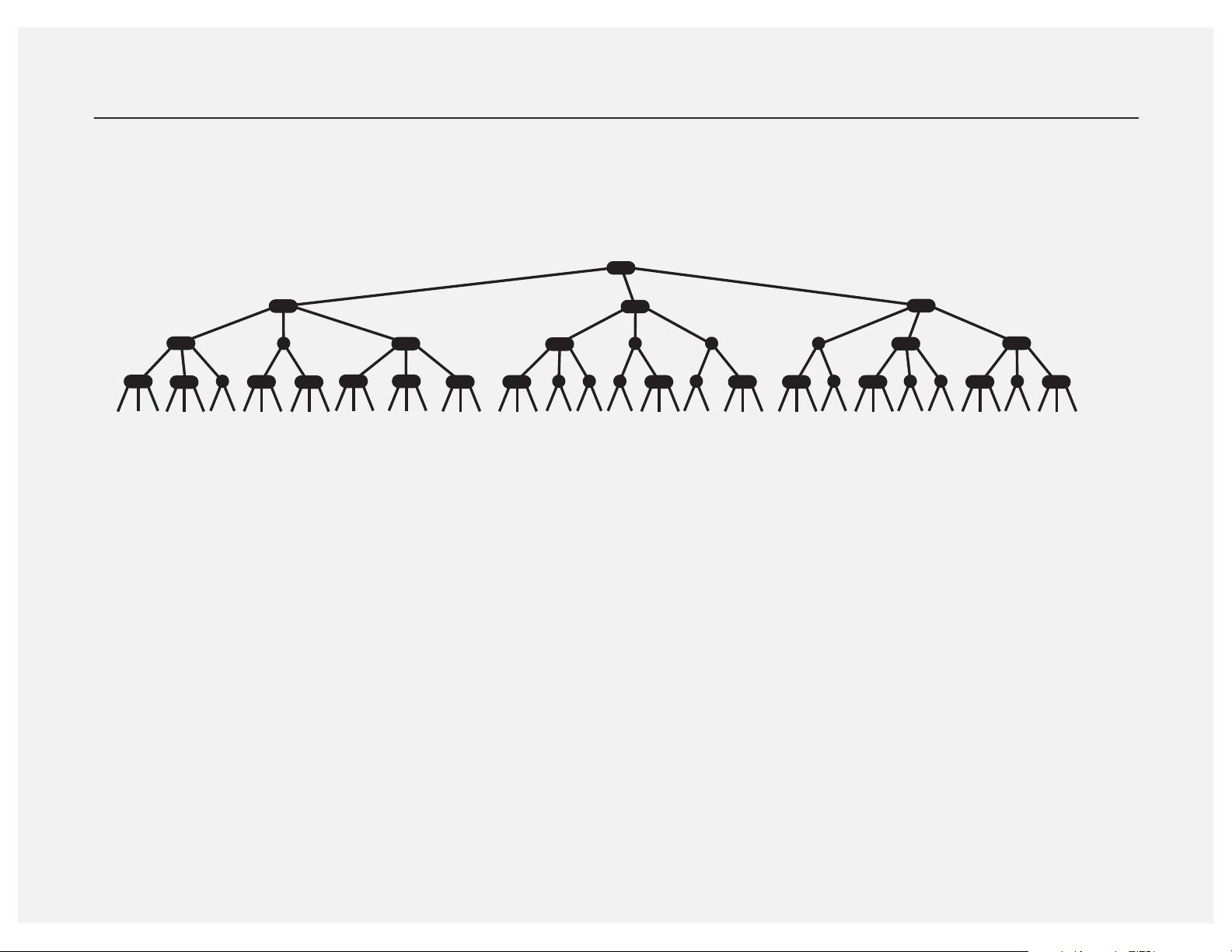 B树则是在大量数据存储和数据库系统中常用的平衡搜索树，特别适用于磁盘等外部存储，因为它的设计考虑到了磁盘I/O效率。B树的每个节点可以包含多个键和子节点，这样在磁盘上能更好地利用空间，减少了访问磁盘的次数。B树的查找、插入和删除操作都能保持近似平衡，且通常具有较好的平均性能。 在算法实现方面，平衡搜索树如红黑树提供了高效的接口，包括搜索、插入和删除操作，平均情况下它们的时间复杂度接近O(log N)。相比于顺序查找和未排序的列表，这些操作在大型数据集上的优势明显。此外，红黑树还支持`compareTo()`方法，用于比较键值，这在构建有序集合时至关重要。 总结来说，平衡搜索树如2-3搜索树、红黑树和B树，通过巧妙的数据结构设计和自调整机制，确保了在大量数据下操作的高效性。学习这些数据结构有助于理解如何在实际编程中优化数据访问性能，尤其是在需要频繁查找、插入和删除元素的场景中。