采样时钟恢复技术在数字用户环路中的应用分析
需积分: 9 62 浏览量
更新于2024-09-11
收藏 1.2MB PDF 举报
"本文主要探讨了数字用户环路（DSL）中的定时恢复技术，特别是针对OFDM（正交频分复用）系统中采用的循环方式。文章详细分析了设计定时恢复功能时的各种权衡，并重点研究适用于MOS LSI（金属氧化物半导体大规模集成电路）技术的方案，目标是在使用回声消除（EC）的情况下，以最小的采样率实现定时恢复。文章主要关注波形差分方法（WDM）作为最优选择，并对其性能进行了深入的理论分析和计算机模拟，对比了二进制和交替标记反转（AMI）线路编码情况下的性能。此外，还提供了描述WDM和连续时间谱线技术二进制抖动性能的闭合形式表达式，用于比较这两种技术的恢复相位和抖动的分析及仿真结果。"
在数字通信系统，尤其是DSL和OFDM系统中，定时恢复是一个至关重要的任务，它确保接收端能正确地同步到发送端的信号，以消除由于采样时钟不同步导致的误码率增加。在DSL系统中，如全双工传输的回声消除和时间压缩复用方法，定时恢复是关键的组成部分，因为这些技术需要处理复杂的信号处理问题，例如回声抵消和频率分复用。
波形差分方法（WDM）是文中推荐的定时恢复技术，其优势在于适合于MOS LSI技术实现，这种技术在降低硬件复杂性和成本方面具有显著优势。WDM通过比较连续采样点的波形差异来检测定时误差，然后调整采样时钟以减小这些误差。在分析WDM的性能时，文章不仅限于理论分析，还采用了计算机模拟，这使得对实际系统性能的理解更加全面。
对于二进制和AMI编码的线路，WDM的表现被详细评估，因为这两种编码方式在DSL系统中常见。闭合形式表达式的提出使得能够定量比较WDM与连续时间谱线技术的性能，特别是在抖动和相位恢复方面。抖动是衡量接收信号相对于理想采样时刻的偏差，而相位恢复则关乎正确解读信号的能力。通过这种方式，作者提供了对不同定时恢复策略的深度理解，有助于优化系统设计并提高通信质量。
这篇文章深入探讨了DSL系统中的定时恢复问题，特别是WDM的应用，这对于理解和改进OFDM系统的性能至关重要，对于通信工程领域的研究和实践具有很高的参考价值。
5
60
IEEE
TRANSACTIONS
ON
COMMUNICATIONS,
VOL.
COM-33,
NO.
6,
JUNE
1985
b"
(
C)
Fig.
'
3.
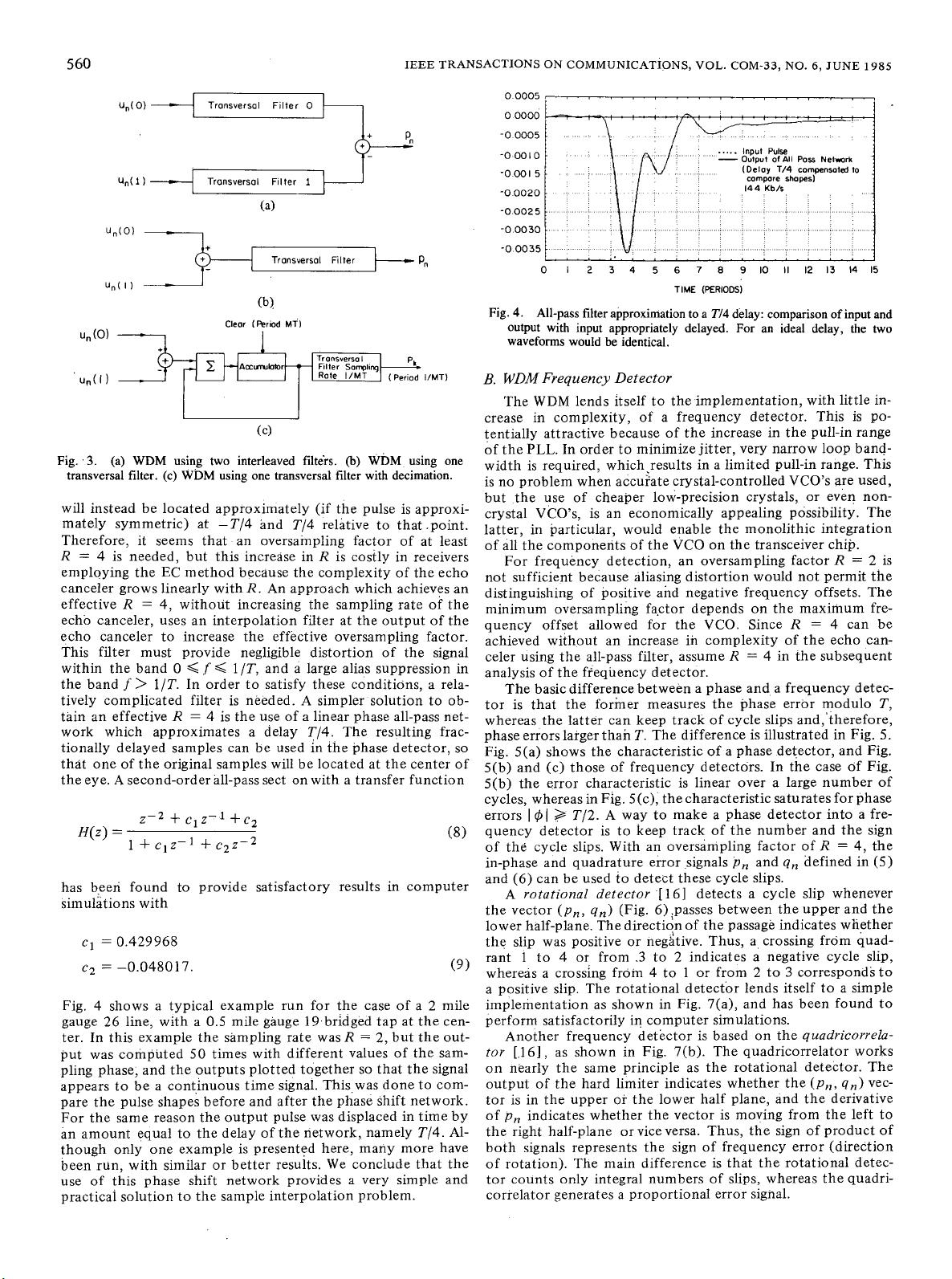
(a) WDM using two interleaved filters.
(b)
WDM
using one
transversal filter. (c) WDM using one transversal filter with decimation.
will instead be located approximately (if the pulse is approxi-
mately symmetric) at -T/4 and T/4 relative to that .point.
Therefore, it seems that an oversampling factor of at least
R
=
4
is needed, but this increase in
R
is costly in receivers
employing the EC method because the complexity
of
the echo
canceler grows linearly with
R.
An approach which achieves an
effective
R
=
4, without increasing the sampling rate
of
the
echo canceler, uses an interpolation filter at the output
of
the
echo canceler to increase the effective oversampling factor.
This filter must provide negligible distortion of the signal
within the band
0
<
f
<
1 /T, and a large alias suppression in
the band
f
>
1/T. In order to satisfy these conditions, a rela-
tively complicated filter is needed. A simpler solution to ob-
tain an effective
R
=
4
is the use of a linear phase all-pass net-
work which approximates a delay T/4. The resulting frac-
tionally delayed samples can be used in the phase detector,
so
that one
of
the original samples will be located at the center of
the eye. A second-order all-pass sect on with a transfer function
z-2
+
c1z-1+
cz
1
+
clz-l
+
czz-2
H(z)
=
(8)
has been found to provide satisfactory results in computer
simulations with
c1
=
0.429968
~2
=
-0.048017.
(3)
Fig. 4 shows a typical example run for the case
of
a
2
mile
gauge 26 line, with a
0.5
mile gauge 19,bridged tap at the cen-
ter. In this example the sampling rate was
R
=
2, but the out-
put was computed
50
times with different values
of
the sam-
pling phase, and the outputs plotted together
so
that the signal
appears to be a continuous time signal. This,was done to com-
pare the pulse shapes before and after the phase shift network.
For the same reason the output pulse was displaced in time by
an amount equal to the delay
of
the network, namely T/4. Al-
though only one example is presented here, many more have
been run, with similar or better results. We conclude that the
use
of
this phase shift network provides a very simple and
practicai solution to the sample interpolation problem.
0.0005
.
,
.
, , ,
, ,
,
.
, ,
,
.
, ,
,
,
0
I23456789101112131415
TIME
(PERIODS)
Fig.
4.
All-pass filter approximation to
a
T/4
delay: comparison of input and
output with input appropriately delayed. For an ideal delay, the two
waveforms would be identical.
B.
WDM Frequency Detector
The
WDM
lends itself to the implementation, with little in-
crease in complexity,
of
a frequency detector. This is po-
tentially attractive because of the increase in the pull-in range
of
the
PLL.
In order to minimize jitter, very narrow loop band-
width is required, which,results in a limited pull-in range. This
is no problem when accurate crystal-controlled VCO's are used,
but the use
of
cheaper low-precision crystals, or even non-
crystal VCO's, is an economically appealing possibility. The
latter, in particular, would enable the monolithic integration
of all the components
of
the VCO on the transceiver chip.
For frequency detection, an oversampling factor
R
=
2 is
not sufficient because aliasing distortion would not permit the
distinguishing
of
positive and negative frequency offsets. The
minimum oversampling factor depends on the maximum fre-
quency offset allowed for the VCO. Since
R
=
4
can be
achieved without an increase in complexity of the echo can-
celer using the all-pass filter, assume
R
=
4 in the subsequent
analysis
of
the frequency detector.
The basic difference between a phase and, a frequency detec-
tor is that the former measures the phase error modulo
T,
whereas,the latter can keep track
of
cycle slips and, therefore,
phase errors larger than
7'.
The difference is illustrated in Fig.
5.
Fig. 5(a) shows the characteristic of a phase detector, and Fig.
5(b) and (c) those
of
frequency detectors. In the case of Fig.
5(b) the error characteristic is linear over a large number
of
cycles, whereas in Fig. 5(c), the characteristic saturates for phase
errors
I @I
2
T/2.
A
way
to
make a phase detector into a fre-
quency detector is to keep track
of
the number and the sign
of
the cycle slips. With an oversampling factor of
R
=
4, the
in-phase and quadrature error .signals
pn
and
qn
defined in
(5)
and (6) can be used
to
detect these cycle slips.
A
rotational detector
.[
161 detects a cycle slip whenever
the vector
(pn,
qn)
(Fig. 6),passes between the upper and the
lower half-plane. The directiqn.of the passage indicates whether
the slip was positive or negatwe. Thus, a, crossing from quad-
rant
1
to 4 or, from
.3
to 2 indicates a negative cycle slip,
whereas
a
crossing from
4
to 1 or from 2 to
3
corresponds to
a positive slip. The rotational detector lends itself to a simple
implementation as shown in Fig. 7(a), and has been found to
perform satisfactorily in computer simulations.
Another frequency detector is based on the
quadricovrela-
tor
[.16], as shown in Fig. 7(b). The quadricorrelator works
on nearly the same principle as the rotational detector. The
output
of
the hard limiter indicates whether the
(P,~,
qn)
vec-
tor is in the upper or the lower half plane, and the derivative
of
pn
indicates whether the vector is moving from the left to
the right half-plane or viceversa. Thus, the sign
of
product
of
both signals represents the sign
of
frequency error (direction
of
rotation). The main difference is that the rotational detec-
tor counts only integral numbers of slips, whereas the quadri-
correlator generates a proportional error signal.
剩余11页未读，继续阅读
点击了解资源详情
点击了解资源详情
101 浏览量
2022-07-15 上传
111 浏览量
138 浏览量
2022-07-15 上传
107 浏览量
119 浏览量
248 浏览量
ejenny1
- 粉丝: 0
- 资源: 7
我的内容管理
展开
最新资源
- 全国计算机技术与软件专业技术资格考试：软件评测师考试大纲
- ajax实战中文版.pdf
- 从头开始对Ubuntu优化
- spring开发指南(夏昕)
- ORACLE9i_优化设计与系统调整
- JTAG调试原理（ARM芯片）
- 第1章 Visual Basic的特点和版本
- KingbaseES入门-Windows
- Oracle DBA应该定期做什么笔记
- 网络工程师PPT 只有第一章 谢谢大家的分享
- 2008年全国计算机等级考试二级公共基础精选120题
- 统计软件SAS教程（李东风）
- 从硬盘安装Linux
- 2007年9月全国计算机等级考试二级C语言笔试试题（含参考答案）.doc
- 统一建模语言(UML)参考手册——基本概念
- 2007年4月全国计算机等级考试二级C语言笔试试题（含参考答案）
