核电子学中的RC微分电路解析：从微分方程到信号转化

"微分方程法解RC微分电路在核电子学系统中的应用涉及到信号与噪声的分析。" 在核电子学系统中，信号处理是至关重要的，尤其是在数据采集和分析过程中。RC（电阻-电容）微分电路是一种常用的电路结构，它能够对输入信号进行微分操作，从而提取出信号的瞬时变化信息。本节重点讨论如何利用微分方程法来解决RC微分电路的问题。 当输入电压Vi(t)为单位冲激函数δ(t)时，我们需要找出对应的输出电压Vo(t)。这个过程包括两个主要步骤：首先，列出电路的微分方程；其次，解这个方程。 1. 列电路方程：在RC电路中，电容C两端的电压变化率与电容上的电压和通过电容的电流有关。利用基尔霍夫电压定律，我们可以得到电路的微分方程。对于一个简单的RC电路，该方程通常是一阶非齐次线性微分方程，形式为： \[ RC\frac{dV_{o}(t)}{dt} + V_{o}(t) = V_{i}(t) \] 2. 解方程：由于输入Vi(t)是δ函数，非齐次项在解方程时会引入特殊解。标准解法是将解分为齐次解和特解两部分。齐次解满足没有输入时的微分方程，而特解则对应于非齐次项。结合这两部分，可以得到Vo(t)的完整表达式。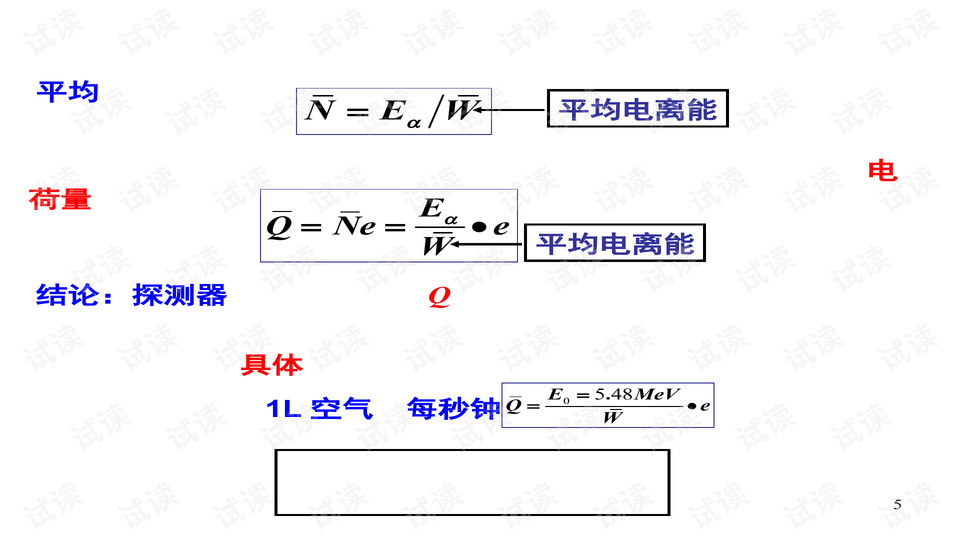 在核电子学中，信号通常由核辐射探测器输出，这些信号是电荷或电流脉冲，具有不同的幅度、形状和随机分布的时间间隔。这些特征反映了探测器对核辐射事件的响应。例如，当α粒子与探测器材料相互作用时，会产生成对的离子，这些离子在电场作用下被收集，形成电信号。信号的大小与入射粒子的能量成正比，而电荷量的测量则有助于计算放射性物质的浓度。 噪声在核电子学中也是一个关键因素，它会影响信号的测量精度。信号与噪声的分析基础涉及理解噪声的来源，如热噪声、散弹噪声等，并研究如何通过滤波和信号处理技术来减小噪声的影响。了解这些基础知识对于设计高效、低噪声的核电子学测量系统至关重要。 微分方程法在解析RC微分电路中的应用，不仅有助于理解电路的行为，还在核电子学测量系统中起到了关键作用。通过对信号和噪声的深入分析，我们可以优化系统性能，提高对核辐射事件的探测和测量能力。