PIPE v2.5：Petri网性能建模工具增强版
5星 · 超过95%的资源 需积分: 9 131 浏览量
更新于2024-09-18
收藏 327KB PDF 举报 "PIPE v2.5 是一个基于Petri网的性能建模工具，由Pere Bonet、Catalina M. Lladó、Ramon Puigjaner和William J. Knottenbelt等人开发。该工具提供了图形化的系统模型可视化，并支持对正确性和性能属性的分析。它是一个免费的、跨平台的开源工具，具有不断扩展的功能。
在Petri网建模形式主义中，系统模型可以方便地以图形化方式展示，同时也能分析其正确性和性能特性。Petri网理论已被广泛应用于各种建模和评估工具的实现。PIPE v2.5是对这一理论的一种实现，它包含了抑制弧的引入，增加了模型的建模能力。抑制弧是一种特殊的边类型，用于阻止令牌的流动，从而在复杂系统中实现更精细的控制。
此外，PIPE v2.5新增了一个分析模块，用于生成并分析系统的瓶颈（siphons）和陷阱（traps）。瓶颈和陷阱是Petri网中重要的概念，它们可以帮助识别系统中的潜在问题和性能瓶颈，通过消除这些瓶颈和陷阱，可以优化系统的性能和稳定性。
用户界面方面也有所改进，提供了更多新功能，使得用户能够更加直观和高效地进行建模工作。这些改进包括增强的交互体验和视觉呈现的提升，使得模型的构建和理解变得更加直观。
论文中，作者通过抑制弧的示例展示了如何使用PIPE v2.5进行系统建模和分析。这证明了新功能的有效性，并强调了PIPE v2.5在性能建模领域的实用性。对于IT专业人士和研究者来说，这一工具不仅提供了一种强大的建模手段，而且因其开源和跨平台的特性，允许用户根据具体需求进行定制和扩展，进一步推动Petri网技术在实际应用中的发展。
PIPE v2.5是一个重要的Petri网工具，它的最新版本在原有的基础上增加了功能，提升了用户体验，对于性能建模和系统分析有着显著的价值。对于那些需要深入理解和利用Petri网技术的人来说，这个工具是一个不可或缺的参考资料。"
A transition is said to be enabled in a marking if each input place contains at least as many tokens as the
multiplicity of the input arc and if each inhibitor place contains fewer tokens than the multiplicity of the
inhibitor arc. Enabled transitions can fire, an atomic action which removes one token from all of its input
places, and generates one token in each of its output places. Figure 1 shows the state of a Petri net before
and after the firing of a transition. When arc weights larger that one are used, the number of tokens required
in each input place for the transition enabling and the number of tokens generated in each output place by
the transitions firing are determined by the weight of the arc connecting the place and the transition.
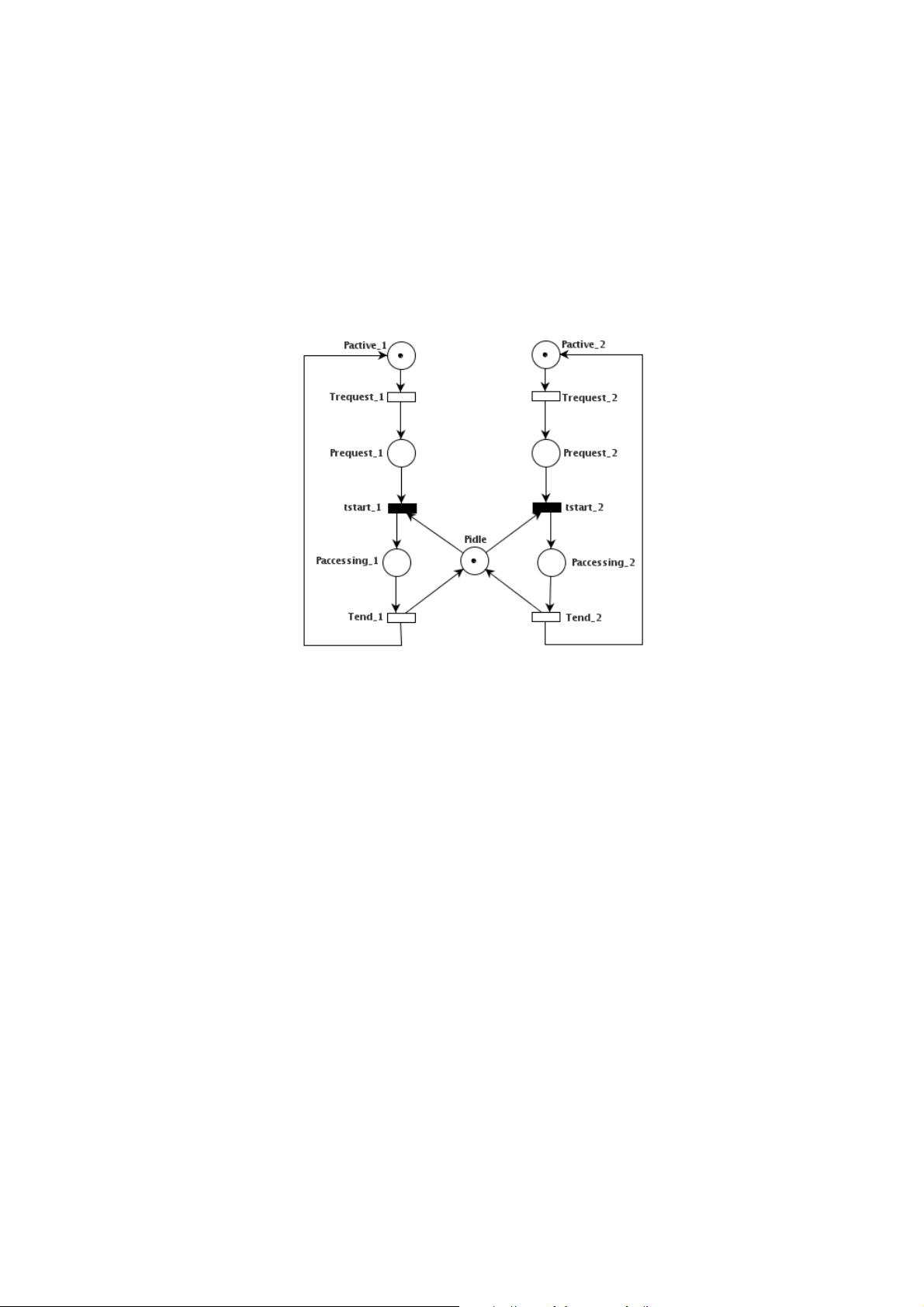
As an example, Figure 2 illustrates a PN that models two processes accessing a shared resource. The
processes can be in one of three possible states: active (doing something that does not involve the shared
resource), requesting the shared resource and accessing the shared resource. The shared resource can be idle
or busy. The initial marking shows that in the initial state both processes are active and the shared resource
is idle.
Figure 2: Producer-consumer GSPN model
Starting with the initial marking, transition occurrences (firings) yield new markings, that in turn give rise
to further transition occurrences. Sequences of transition occurrences (also called occurrence sequences) are
used to define qualitative (or behavioral) properties of PNs, such as deadlock freedom (no total deadlock
is reachable), liveness (no partial deadlock is reachable), boundedness (on each place the number of tokens
cannot grow in an unlimited way), and the existence of home states (markings that can always be reached
from any reachable state). Occurrence sequences are normally represented as a marking graph, which is an
arc-labelled directed graph with a distinguished initial vertex and edges labelled by transitions: the vertices
are the reachable markings, the distinguished initial vertex is the initial marking, labelled edges are all triples
(m, t, m
0
) such that m and m
0
are reachable markings satisfying m
t
−→ m
0
.
2.1 Generalized Stochastic Petri Nets
We are interested in the so-called Generalized Stochastic Petri Nets (GSPN) which are characterized by 2
types of transitions:
• Stochastic transitions: associated with an exponentially distributed firing delay.
• Immediate transitions: associated with a null firing delay.
Formally, a GSPN can be defined as follows:
3
剩余11页未读，继续阅读
2020-11-04 上传
2014-03-28 上传
2015-02-08 上传
2021-04-30 上传
2021-04-25 上传
2021-02-16 上传
2021-05-13 上传
