二维共形场论中的拓扑缺陷线与重整化群流分析

146 浏览量更新于2024-07-16 收藏 1.86MB PDF 举报

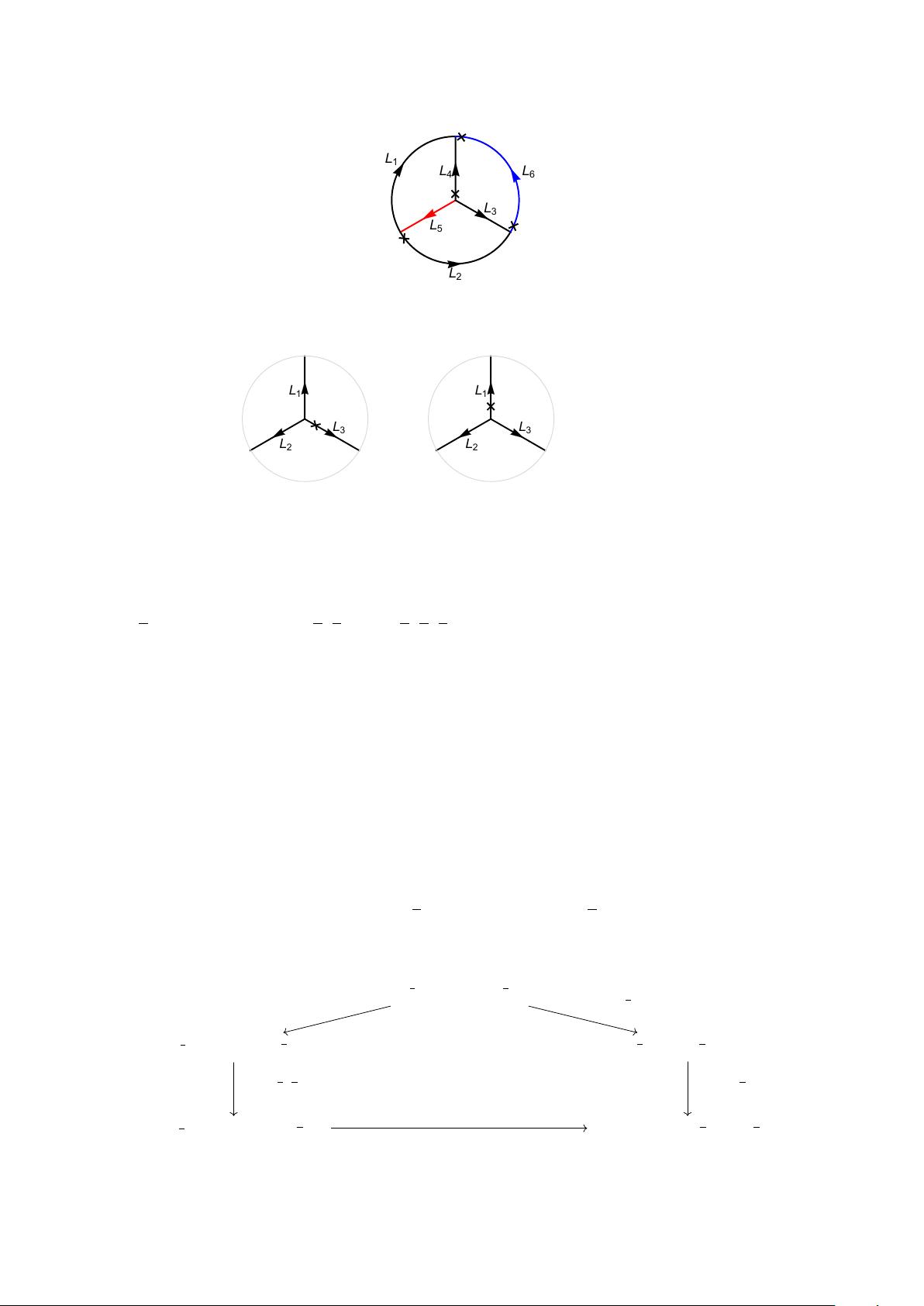
"二维中的拓扑缺陷线和重归一化组流" 在二维共形场理论（CFT）的研究中，拓扑缺陷线（TDLs）是一个关键的概念。拓扑缺陷线是一种特殊的物理对象，它能够概括全局对称性和Verlinde线，并且包含了它们的融合类别，而无需依赖编织操作。这些TDLs携带的缺陷算符是理解这类模型的核心要素。论文深入探讨了TDL的交叉关系，这是理解它们如何相互作用和影响系统的关键。这种交叉关系与非霍夫特异常紧密相关，非霍夫特异常是量子场论中一种重要的对称性破缺现象。通过分析这些异常，我们可以更深入地理解CFT的结构和性质。作者进一步研究了TDL在重归一化组流（RG流）中的行为。RG流描述了量子场论在不同尺度下的演化，特别是从紫外（高能量）到红外（低能量）的行为。他们指出，如果在RG流中保留某些不可逆的TDL，那么系统的真空状态不能是简并的带隙状态。这是一个重要的限制，因为带隙状态通常与有序相和稳定阶段相关联。对于不同的RG流量，研究者利用TDL和模块不变性来完全确定红外端（低能量极限）的拓扑量子场论（TQFT）。TQFT是一种具有严格拓扑不变性质的量子场论，它们在物理学和数学中有许多应用，特别是在统计力学和凝聚态物理中。此外，文章还讨论了如何使用TDL来约束RG流，确保它们只能终止于特定的共形临界点或TQFT。这种方法为理解CFT和TQFT之间的关系提供了一种新视角，同时也为探索新的量子相变和临界行为提供了工具。这篇论文通过深入研究TDLs在二维CFT中的作用，揭示了它们在理解和分类量子场论中的重要作用，尤其是在描述非平凡的相变和RG流的性质方面。通过对TDL交叉关系、非霍夫特异常和模块不变性的研究，论文为理论物理学家提供了一套强大的分析工具，促进了对量子世界深层次理解的进步。

JHEP01(2019)026

Figure 11. The H-junction crossing kernel K

, L

) represented as the correlation functional

of the Mercedes graph.

◦ C

Figure 12. The cyclic permutation map on a T-junction.

crossing kernels that relate H-junctions in the 12 → 34 channel to those in the 23 →

41 channel.

The map K

, L

) regarded as a multi-linear complex-valued function on

⊗ V

, is the same as the correlation functional of

the Mercedes TDL graph in ﬁgure 11.

2.2.2 Pentagon identity

It follows from the locality property applied to a TDL graph on the disc with ﬁve external

lines crossing the boundary that the H-junction crossing relations must obey the pentagon

identity. Using the cyclic permutation map

: V

→ V

(2.7)

on T-junction vector spaces as in ﬁgure 12, the permuted H-junction crossing kernels

K is

related to K by

, L

) ≡ C

◦ K

, L

) ◦ C

: V

⊗ V

→ V

⊗ V

(2.8)

such that they appear in the H-junction crossing relations as depicted in ﬁgure 13.

As illustrated by the following commuting diagram,

⊗ V

j,j

⊗ V

j,k

⊗ V

j,k

(

)

(j,j

)

(

)

(j,

)

– 12 –

JHEP01(2019)026

simple L

◦

, L

)

Figure 13. The permuted crossing kernel

K. Note that the last legs at the T-junctions are marked

diﬀerently in comparison to the crossing kernel K deﬁned in ﬁgure 10.

the permuted crossing kernels

K satisfy the pentagon identity

, L

) ◦

, L

)

, L

) ◦

, L

) ◦

, L

(2.9)

In the above diagram, we abbreviated

, L

) by

, j

), and V

by V

The admissible crossing relations are classiﬁed by the solutions to the pentagon identity.

The solutions are rigid in the sense that they admit no continuous deformation, modulo the

gauge transformations corresponding to the change of basis vectors in each junction vector

space (see appendix A). This is a proven property in category theory known as Ocneanu

rigidity [42]. Since the solution set is discrete, a solution cannot change continuously under

the RG ﬂow, and hence the crossing relations should match between the UV and the IR

theories. This is a key property that will be used later to constrain various RG ﬂows.

2.2.3 Action on bulk local operators and defect operators

Given a TDL L, let

L : H → H be the linear operator on the bulk Hilbert space H

of the CFT on the cylinder deﬁned by wrapping an L loop around the spatial circle.

Assuming no isotopy anomaly, we can think of

L as an operation on a bulk local operator

φ by contracting an L loop encircling φ.

As already mentioned, the isotopy invariance

property implies that

L preserves the conformal weight of φ. More generally, as shown

in ﬁgure 14, contracting a TDL L loop on a bulk local operator φ, where L has another

TDL L

attached to it with a junction vector v, produces a defect operator (

· φ) in

of the same conformal weight as φ. We refer to this operation as “lassoing” for its

resemblance. Note that the information of L

is implicit in the notation of

: H → H

since v ∈ V

,L,L

. A similar lassoing can be performed when the TDL loop circles a defect

operator, as in ﬁgure 15. Combined with crossing (partial fusion), passing a bulk local

operator (or a defect operator) through a TDL L generally introduces a T-junction that

ends on a defect operator, as shown in ﬁgure 16.

In the presence of isotopy anomaly,

L diﬀers from the left of ﬁgure 14 by a phase, a scenario which we

ignore for the moment, and return to in section 2.4.

– 13 –

JHEP01(2019)026

bution hLie

πc

12t

from the one ground state.

In this limit, (2.12) reduces to

hLi = lim

t→0

−

πc

12t

−2πt(L

−

)

≥ 0 . (2.13)

An important corollary of the locality property is that the set of hLi satisﬁes a system

of polynomial equations with positive integer coeﬃcients, given by the abelianization of

the fusion ring. In a unitary, compact CFT, this leads to the stronger constraint

hLi ≥ 1,

(2.14)

since by compactness we expect hLi for all TDLs L to be bounded below by a positive

number.

Had there been any L with hLi < 1, the sequence of TDLs L

with n ∈ N

would go to zero and hence violate this condition.

Furthermore, since hLi satisﬁes the polynomial equations, it is protected under RG

ﬂow. In the case where there are degenerate vacua in the IR, hLi is deﬁned as the cylinder

expectation value in the vacuum inherited from the UV.

Given the expectation (2.14), we can run the modular invariance argument in reverse

to argue that in a unitary, compact CFT with a unique vacuum, the Hilbert space H

defect operators at the end of a TDL L must always be non-empty,

6= ∅.

(2.15)

Importantly, if we relax the condition of a unique vacuum, then there could be TDLs on

which no defect operator can end. We will encounter such an example in some TQFTs

with degenerate vacua in section 7.2.3.

Let us also introduce the expectation value of an empty clockwise L loop on the plane,

which we denote by R(L), and the expectation value of a counterclockwise L loop, which we

denote by R(L). The expectation value on a plane R(L) might not equal to the expectation

value on a cylinder hLi. Their relation will be discussed in section 2.4.

A bulk local operator φ is said to commute with a TDL L if they commute as operators

on the cylinder. In particular, this requires

L|φi = hLi|φi. (2.16)

In unitary theories, (2.16) further implies that

· φ = 0. To see this, we start with the

conﬁguration in ﬁgure 17. Next we glue two copies of the diagrams in ﬁgure 17 together

by summing over the states in H

L,L

and obtain the relation in ﬁgure 18. The correlation

This argument also holds in non-unitary CFTs, where the ground state may not correspond to the

identity operator, as long as the degeneracies are non-negative (e.g., no ghost). For example, in the Lee-

Yang model, a.k.a. the (2,5) minimal model, the limit t → 0 of Z

(−1/τ, −1/¯τ) is dominated not by the

identity operator, but by the primary of weight (−

, −

Using the folding trick, one can relate the TDL L in a CFT T to a boundary state B in the tensor

product CFT T ⊗ T . Furthermore hLi maps to the g-function of B (log g being the boundary entropy).

When T ⊗T is described by a nonlinear sigma model, for instance, B corresponds to a D-brane wrapping a

submanifold of the target space whose mass is proportional to the g-function. Thus a vanishing g can only

occur in a singular sigma model. More generally, we expect the g-function, and hence hLi, to be bounded

from below by a positive number in any unitary, compact CFT.

– 15 –

剩余84页未读，继续阅读

weixin_38653508

粉丝: 2
资源: 903

二维共形场论中的拓扑缺陷线与重整化群流分析

具有高阶张量重归一化组的二维Ising模型的相变

全息痕迹异常和局部重归一化组

功能重归一化组方法实现颜色超导相变

二维非阿贝尔希格斯模型的张量重整化组研究

C++一维数组二维数组写入txt，从txt中读取数据存到一维数组二维数组

二维二分类的数据

Java 实现二维条码， 这是一个Java 包，二维条码使用

全息重归一化与超对称：解析边界理论的分歧与统一

二维不可压缩流体流动：涡量流函数法源代码解析

MATLAB基础绘图教程：一维曲线与二维曲面

最新资源

Java 实现二维条码，这是一个Java 包，二维条码使用