多元线性回归模型检验与Stata应用详解
需积分: 9 11 浏览量
更新于2024-06-30
收藏 684KB PPT 举报
第三讲主要探讨了多元线性回归模型的检验方法以及Stata软件在这一领域的应用。本章节涵盖了关键知识点:
1. **拟合优度检验**:
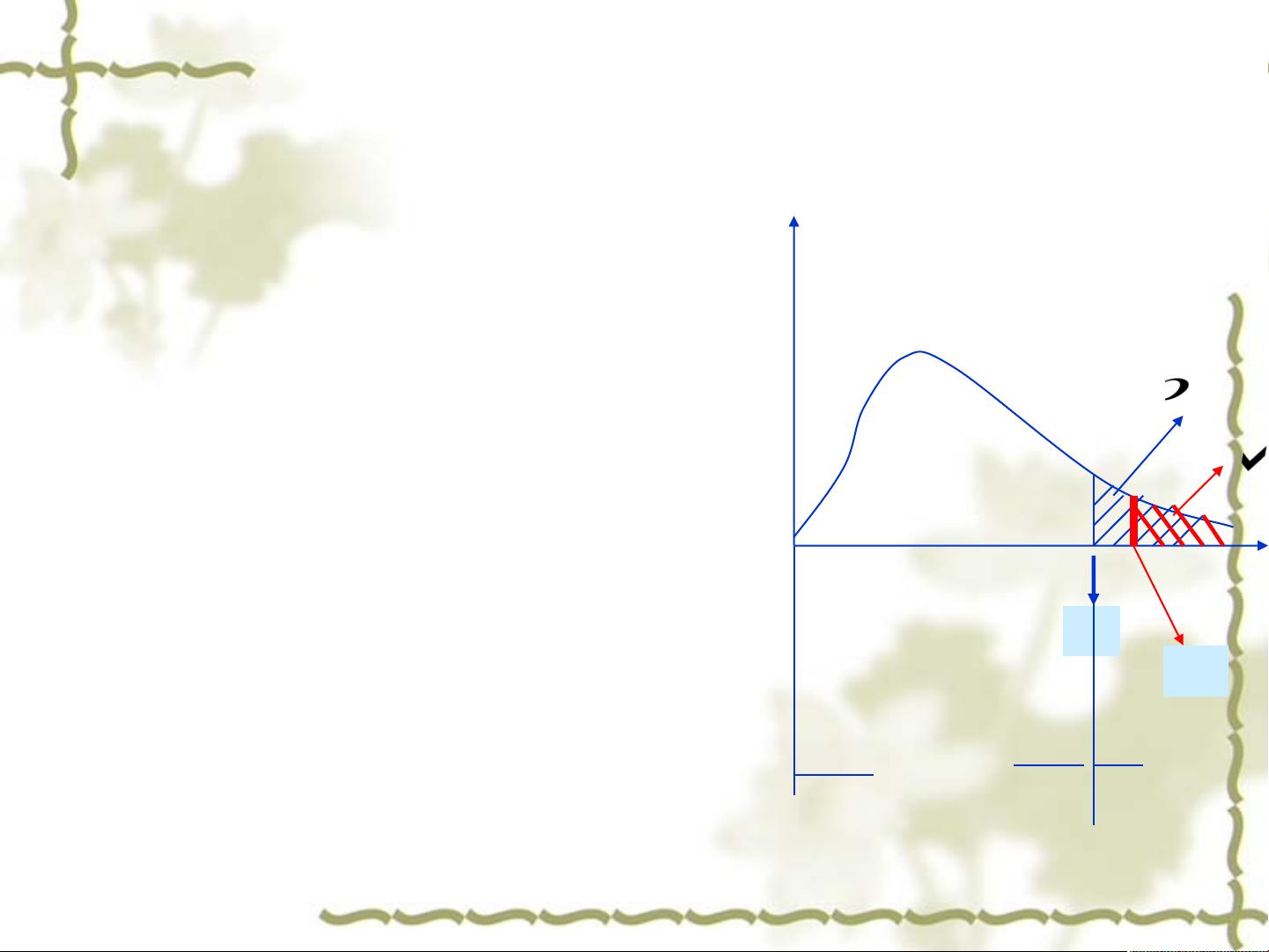
- 可决系数(R²)与调整的可决系数(Adjusted R²)是衡量模型拟合程度的重要指标。R²表示模型解释因变量变异性的比例,而调整R²考虑了自变量数量对拟合度的影响,防止过度拟合。总离差平方和(Total Sum of Squares, TSS)分为观测值对均值的离差平方和(TSS)、拟合值对均值的离差平方和(Explained Sum of Squares, ESS)和观测值对拟合值的离差平方和(Residual Sum of Squares, RSS)。当模型的R²接近1时,说明模型拟合良好。
2. **可决系数**:
- 可决系数等于1减去残差平方和(RSS)占总离差平方和(TSS)的比例,表示模型解释了因变量变化的百分比。模型中的解释变量越多,理论上R²会增大,但仅增加变量并不一定能提高模型质量,调整R²可以更准确地评估变量的重要性。
3. **调整的可决系数计算**:
- 在固定样本容量下,随着解释变量(k)增加,自由度减少。通过调整的R²公式,可以平衡模型复杂性和拟合度,确保在增加变量时,不单纯因为变量数量增多而提高R²。
4. **方程显著性检验(F检验)**:
- F检验用于整体评估模型参数的显著性,即所有解释变量对因变量是否有共同影响。它比较的是残差平方和的自由度与解释变量的自由度乘积(F统计量),如果F统计量大于预定的临界值,说明模型的整体显著性存在。
5. **误区与现实**:
- 在实际应用中,人们可能会误以为增加变量会自动提升模型的拟合效果,但R²的增大会受到变量数量的影响。因此,评估模型的质量不仅要看R²,还要考虑调整后的R²,并结合专业知识来选择最合适的变量组合。
通过Stata软件,这些检验可以通过内置命令方便地执行,帮助用户深入理解并优化多元线性回归模型。在实际操作中,正确运用这些统计工具能有效提高模型的可靠性和实用性。
点击了解资源详情
2023-05-01 上传
智慧安全方案
- 粉丝: 3836
- 资源: 59万+
最新资源
- 行业分类-设备装置-一种具有储气装置的硬质合金冷却过滤设备.zip
- Star-Wars-Website:这是一个练习
- RF 一分八 SWITCH(0-6G).zip
- Auth0Test
- 行业分类-设备装置-一种六齿轮复杂轮系可变换教具.zip
- linked_list
- vc6开发的sip软交换
- ovn-ontology:这是一个使用http构建的本体
- ms-dropdown-rails:将ms-下拉列表添加到您的Rails资产管道中
- Zer0sum:我正在尝试用统一游戏引擎制作我的第一个(不是真的)二维平台游戏
- speedprogramming_pteufl
- Robinhoot:Robinhood的可视化Web应用程序和核心功能的副本,这些功能利用Ruby on Rails和IEX Cloud API
- 行业分类-设备装置-一种全自动调节式防伪纸张过数装置及方法.zip
- pwa_shop-finder
- MvgSoft:来自运动的结构
- sigProject