高效构建后缀数组与高度数组

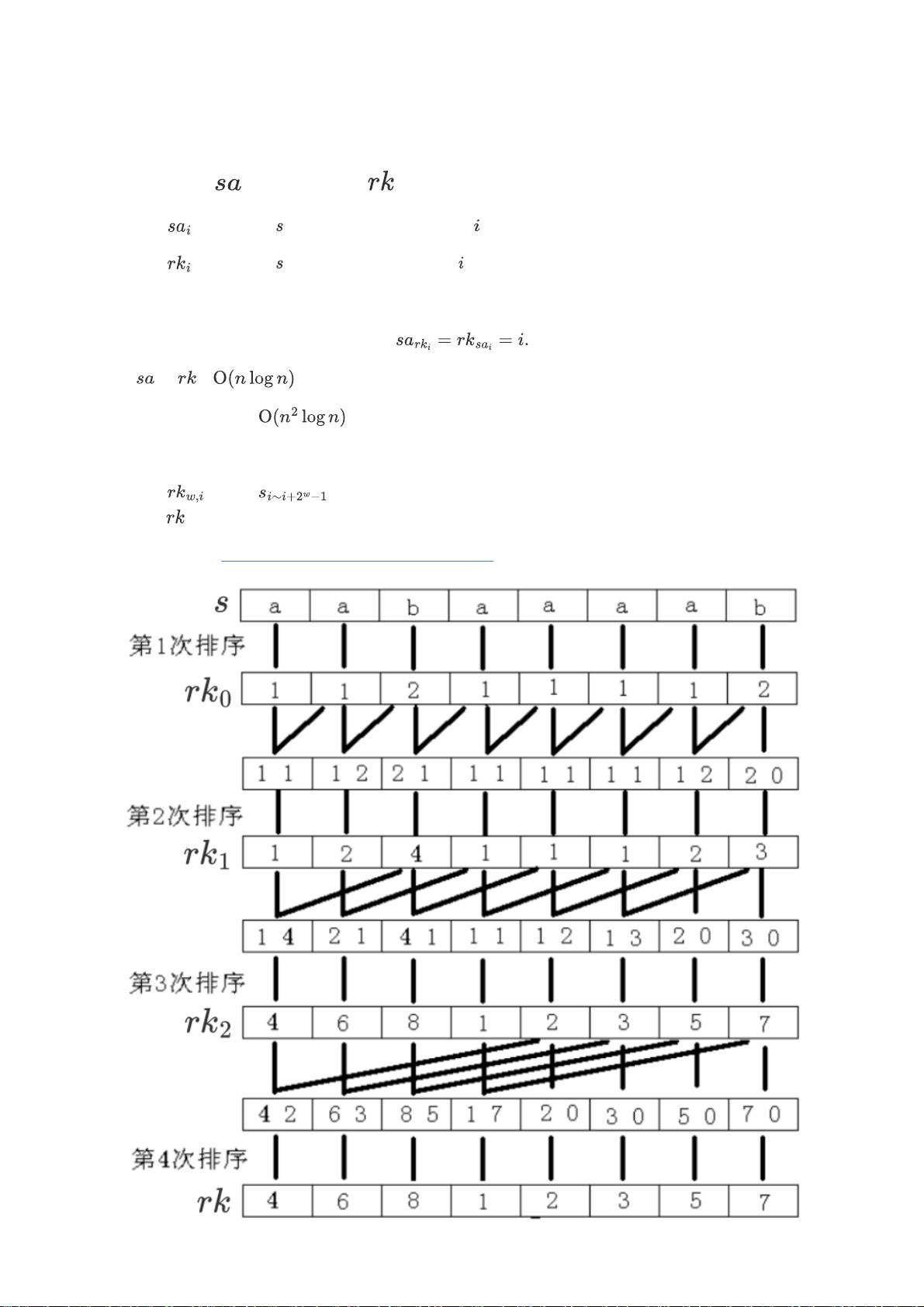
"这篇资源是一份关于后缀数组的学习笔记，详细介绍了后缀数组的定义、构建方法以及高度数组（LCP数组）的计算过程，适用于想要深入理解字符串处理算法的编程爱好者和学习者。通过倍增思想和双关键字排序策略，实现了高效地构建后缀数组，同时利用引理证明了求解LCP数组的有效性。" 后缀数组是一种数据结构，用于高效地处理字符串的相关问题，例如查找子串、模式匹配等。它将一个字符串的所有后缀按照字典序排序，存储在一个数组中。在给定的笔记中，作者首先定义了后缀数组的概念，并指出直接排序所有后缀是不实际的，因为这样会涉及 O(n^2) 的复杂度，对于大数据量的字符串来说无法接受。 为了优化排序过程，笔记提到了倍增思想，通过多次合并子串的排名（rank）来逐渐构建完整的后缀数组。在每次倍增过程中，使用基数排序或计数排序对后缀进行排序。其中，基数排序可以处理字符的ASCII值范围（如256种可能的字符），而计数排序则用于快速统计每个字符出现的次数。此外，笔记中还提到，第二个关键字的排序可以避免使用计数排序，直接按值加入，从而简化了排序步骤。 高度数组，也称为LCP（Longest Common Prefix）数组，记录了相邻两个排序后后缀的最长公共前缀的长度。笔记通过引理证明了如何递归地计算LCP数组。具体步骤包括初始化，使用字符频率数组b进行预处理，然后通过双关键字排序更新后缀的位置。在这个过程中，通过倍增宽度w逐步处理后缀，直到w覆盖整个字符串。 在构建后缀数组的过程中，笔记中的代码展示了如何迭代地更新和排序后缀，以及如何使用计数排序进行优化。在最后一段，可以看到代码片段中如何保存和恢复rk数组的值，这是在多轮排序中保持信息的关键。 这份学习笔记详细解释了后缀数组和高度数组的构造原理，对于理解字符串处理算法和实际编程应用具有很高的参考价值。适合正在学习数据结构、算法或者准备面试的编程学习者阅读和实践。