正负法圆弧生成：插补算法原理与应用

正负法画圆弧是一种基于平面区域分类的图形生成算法，它将平面上的圆点划分为三个区域：G-（函数f(X,Y)小于零的区域）、G0（函数值等于零的边界）和G+（函数值大于零的区域）。这种方法利用了函数的符号来决定图形的绘制顺序，通过逐层扫描这些区域并根据函数值的正负切换图形的生成方式，从而生成精确的圆弧。 在第四章的基本图形生成算法中，图形生成的关键在于将抽象的数学模型转化为实际的像素集合，也就是所谓的图形扫描转换或光栅化过程。这个过程包括两个主要步骤：首先确定每个像素的位置，然后根据图形的颜色或属性执行写入操作。图形的生成元素主要包括点、直线、圆和曲线，以及它们的几何信息、非几何信息和指针信息。 点是基础图形元素，其位置通常用二维坐标（x, y）表示，可以扩展到三维空间。直线和曲线的生成涉及到坐标系的转换，如用户坐标系、笛卡尔坐标系（直角坐标系）、设备坐标系（如屏幕或绘图仪坐标系）和规范坐标系，后者是为了设备独立性和信息交换的便利。 在扫描转换算法的一节中，坐标系的概念至关重要。用户坐标系灵活且不拘泥于物理设备，而设备坐标系则紧密关联硬件特性。笛卡尔坐标系和设备坐标系之间的转换通常涉及屏幕坐标的标准化处理，确保图形在屏幕上正确显示。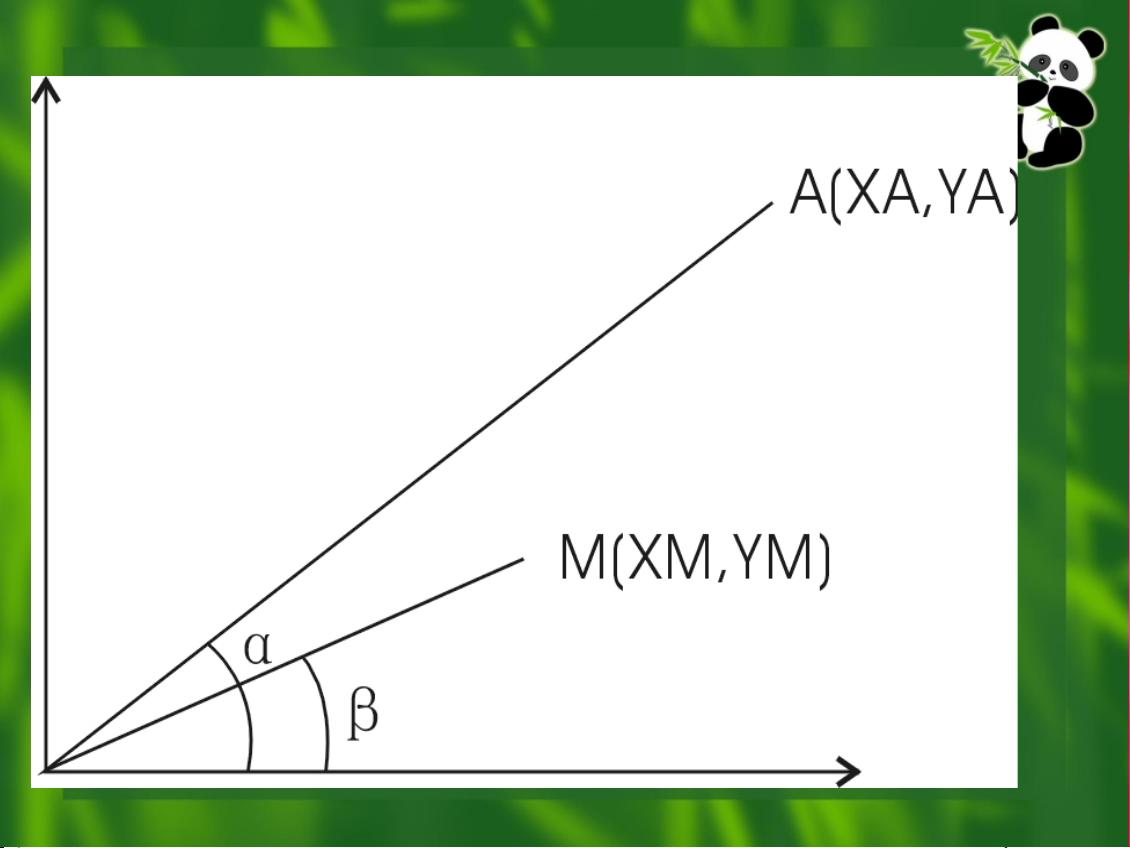 圆弧的生成是通过将圆的参数方程映射到笛卡尔坐标系中，然后利用正负法确定每个像素是否属于圆弧路径。这种方法允许精确控制圆弧的绘制，对于计算机图形学中的图形渲染和动画制作来说，正负法画圆弧是一项基础且重要的技术。 总结来说，正负法画圆弧是计算机图形学中的一个实用工具，它通过数学分析和图形扫描转换，实现了从数学模型到像素集合的转换，是实现图形细腻绘制的关键步骤之一。理解并掌握这一方法，对于理解和实现图形生成算法，尤其是在计算机辅助设计（CAD）和计算机图形学领域，具有重要意义。