三分法求解凸性函数极值问题

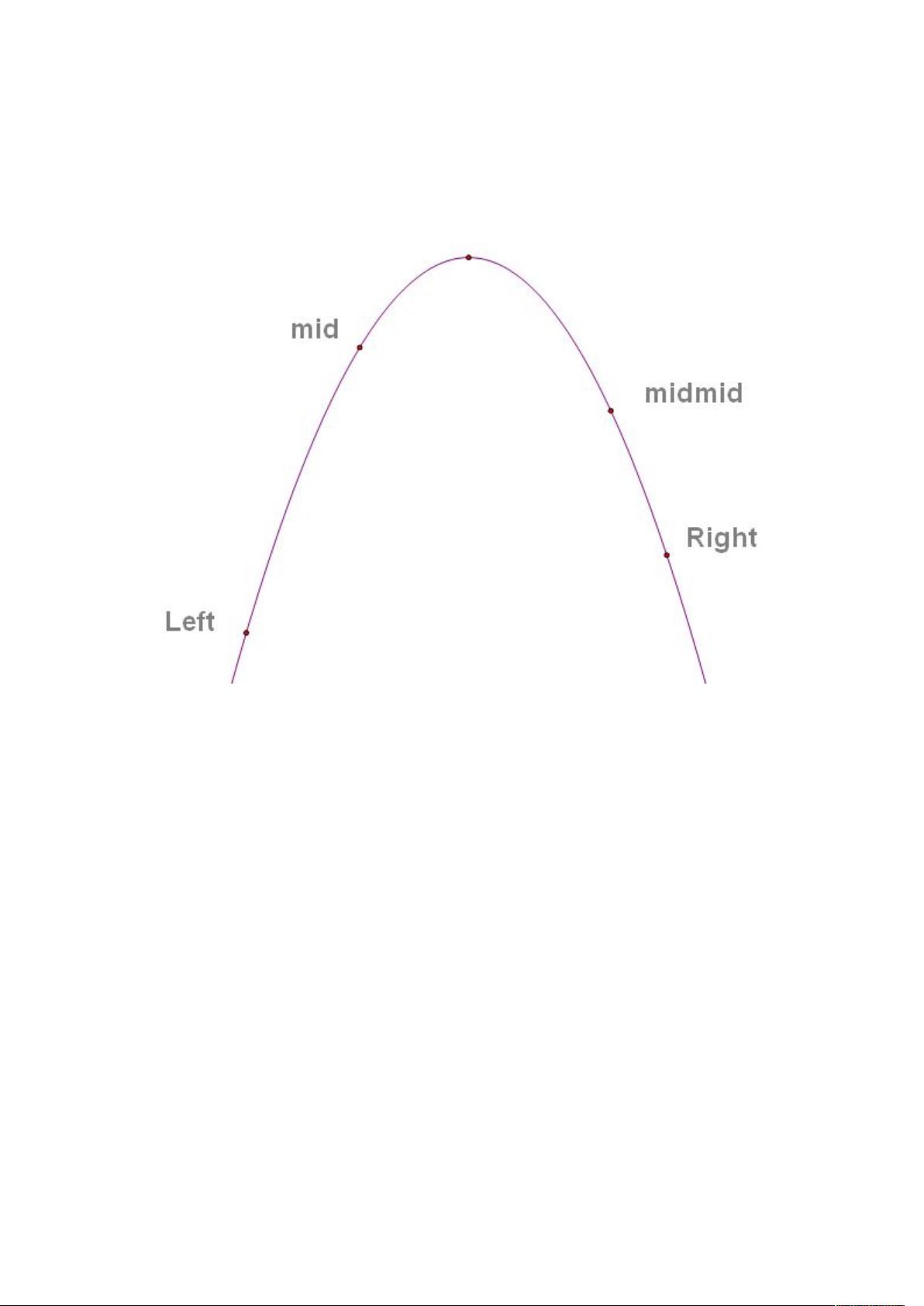
"三分法是一种在处理凸性函数时寻找极值点的算法，与二分法相似，但更适用于非单调的凸函数。本文通过分析具体的编程模板和实例题目来探讨三分法的应用。 三分法的基本思想是通过不断将搜索区间分为三等份，根据函数在中间两个点的相对大小来调整搜索范围。当函数是凸函数时，其极值通常位于区间的一端或内部的一个特定位置。与二分法不同，二分法只考虑区间的中点，而三分法则考虑中点及其相邻的一半区间，从而更快地收敛到极值点。 程序模板通常包含两个关键部分：`Calc`函数和`Solve`函数。`Calc`函数负责计算给定点的函数值，而`Solve`函数执行三分法的迭代过程。在`Solve`函数中，初始化左右边界`Left`和`Right`，然后在循环中计算`mid`和`midmid`，这两个点分别位于当前区间的中点和三分之二点。比较`mid`和`midmid`处的函数值，根据比较结果更新搜索区间。 以给出的两个实例题目为例： 1. `buaa1033EasyProblem`： 题目要求找到在线段上使点P到该点距离最小的点。这是一个典型的凸函数问题，因为距离函数在直线段上是凸的。通过三分法，我们可以逐步缩小搜索范围，找到距离最小的点。 2. `ZOJ3203LightBulb`： 这个问题涉及到光线投射形成的影子长度。当灯、人的头部和墙角形成直角时，影子的地面部分达到最长。同样，这是一个凸函数问题，因为随着人向左或向右移动，影子的最长长度在某个特定位置达到最大。 通过这些实例，我们可以看到三分法在实际问题中的应用，特别是在优化问题中寻找局部极值。对于凸函数，三分法比二分法具有更快的收敛速度，因为它能更快地排除掉不包含极值的区间。在编写三分法的程序时，注意循环条件通常是`Left + EPS < Right`，其中`EPS`是一个很小的正数，用于处理浮点数精度问题。 总结来说，三分法是解决凸性函数极值问题的有效工具，尤其在二分法不适用的情况下。通过理解和掌握三分法，可以解决许多实际场景中的优化问题，比如上述的找点距离最小化和影子长度最大化问题。"