MATLAB非线性拟合实战：从散点图到最佳参数

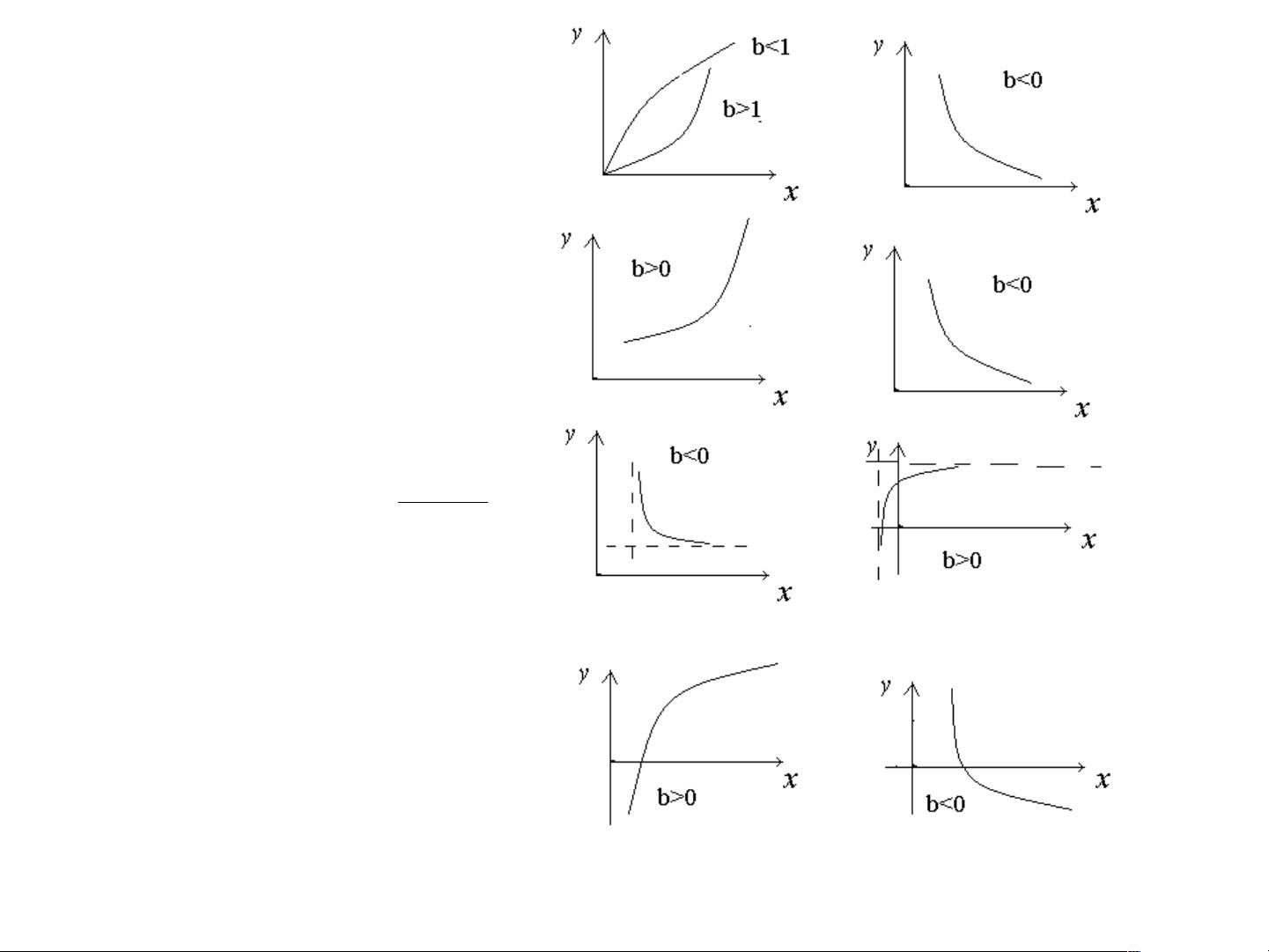
"该资源为matlab非线性拟合的课件，旨在教导如何使用MATLAB进行非线性拟合处理，适用于处理各种非线性数据，如多项式、指数、对数、幂和S形曲线等。通过最小二乘法确定最佳参数，并用可决系数评估拟合质量。课件提供了具体示例和代码，包括计算可决系数的MATLAB代码，以及不同类型的非线性函数及其对应的数学表达式。" MATLAB中的非线性拟合是一种数据分析技术，用于寻找最能描述数据趋势的非线性函数。这个过程通常涉及以下几个关键步骤： 1. **数据可视化**：首先，通过绘制散点图来观察数据分布，这有助于初步判断可能的函数类型。 2. **函数选择**：基于数据的形状，选择一个合适的非线性函数模型，如多项式、指数、对数、幂函数或特定的非线性方程，如罗杰斯蒂模型、龚帕兹模型、理查德模型和威布尔模型等。 3. **初始参数估计**：确定待定参数的初始值，这是优化过程的起点。 4. **最小二乘法**：使用MATLAB内置的`lsqcurvefit`函数或其他优化工具，通过最小化观测数据与拟合函数之间偏差的平方和来找到最佳参数。目标是最小化以下表达式： \( \sum_{i=1}^{n}(y_i - f(x_i))^2 \) 其中\( y_i \)是观测值，\( f(x_i) \)是用待定参数表示的模型预测值，\( n \)是数据点的数量。 5. **拟合质量评估**：计算可决系数\( R^2 \)，其定义为： \( R^2 = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2} \) 其中，\( \hat{y}_i \)是拟合值，\( \bar{y} \)是所有观测值的平均值。\( R^2 \)越接近1，表示拟合效果越好。 6. **代码示例**：MATLAB中计算可决系数的代码如下： ```matlab x=[2:16]; y=[6.42,8.2,9.58,9.5,9.7,10,9.93,9.99,10.49,10.59,10.6,10.8,10.6,10.9,10.76]; y1=x./(0.1152+0.0845*x);%拟合曲线 R2=1-sum((y-y1).^2)/sum((y-mean(y)).^2) ``` 这段代码展示了如何计算给定数据的拟合曲线的可决系数。 7. **应用与实例**：非线性拟合广泛应用于各种科学和工程领域，如生物统计学（如生长曲线）、物理学（如光谱分析）和工程学（如信号处理）等。 通过这个课件，学习者将能够掌握如何在MATLAB环境中有效地执行非线性拟合，从而更好地理解和分析非线性数据模式。