PID控制原理与数字PID算法解析

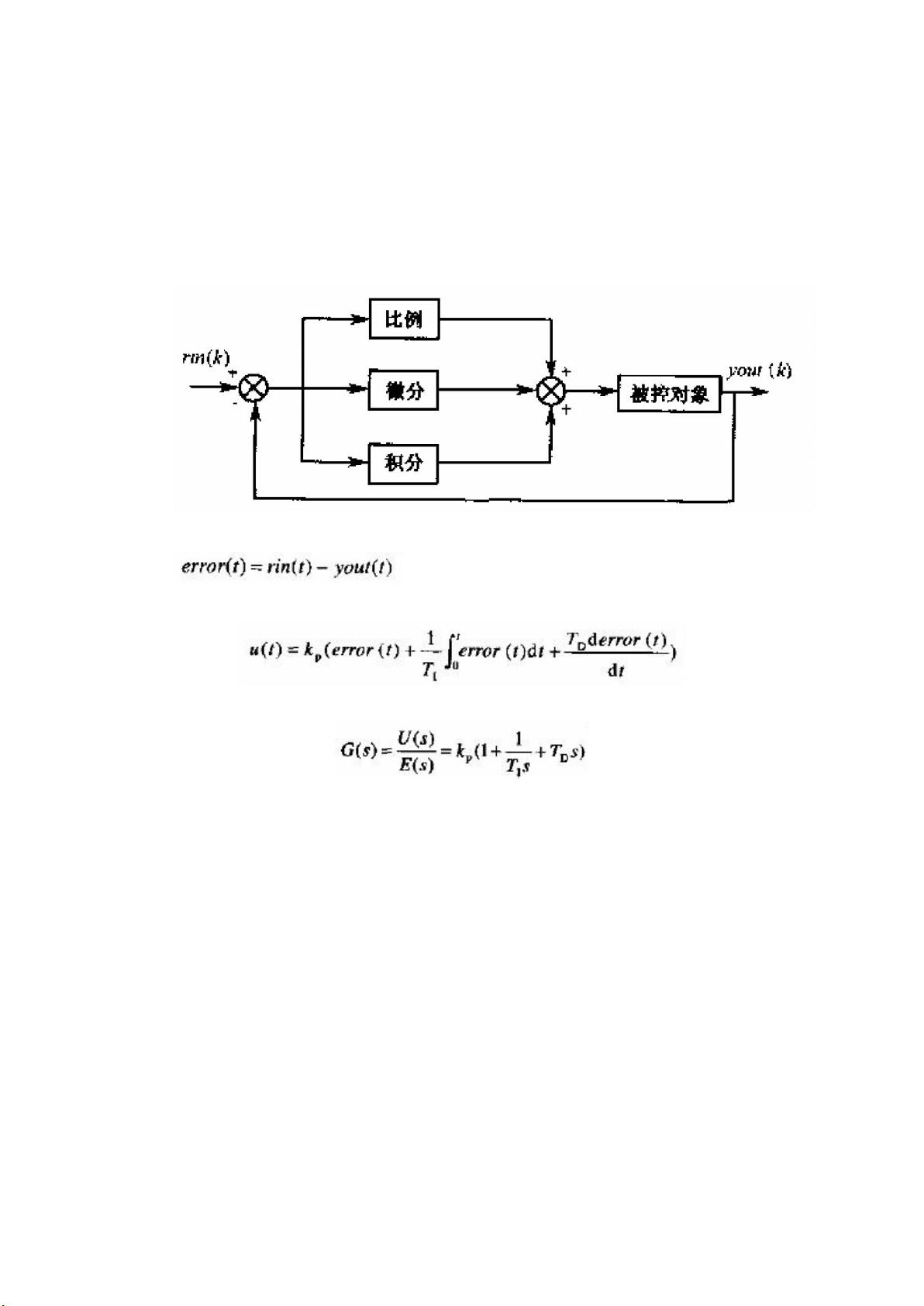
"PID控制及其应用.pdf" PID控制是一种广泛应用的闭环控制策略，它结合了比例（P）、积分（I）和微分（D）三个控制元素，以改善系统的响应性能和稳定性。这种控制方法最早起源于模拟控制系统，现在广泛应用于数字控制系统，尤其是在FPGA（Field-Programmable Gate Array）等硬件平台上实现。 在PID控制中，比例项(P)对当前偏差做出即时反应，它的输出与偏差成正比，可以快速调整控制量以减小偏差。积分项(I)则关注偏差的累计，随着时间的推移，积分作用会消除静态误差，提高系统的无差度。积分时间常数(Ti)决定了积分作用的强度，较大的Ti会使积分作用较弱，而较小的Ti则会增强积分效果。微分项(D)则是基于偏差变化率的预测，它能提前对系统进行调整，以减少调节时间和提高响应速度。微分时间常数(Td)决定了微分作用的敏感度。 在模拟PID控制系统中，这三个参数（Kp、Ti、Td）可以通过调整硬件电路的元件值来设定。而在数字PID控制中，这些参数通常在软件中配置。数字PID有两种主要形式：位置式和增量式。位置式PID算法的输出直接反映了执行机构的位置，可能对干扰敏感。相比之下，增量式PID仅计算控制增量，常用于电机控制，因为它能更好地平滑输出并减少响应中的振荡。 增量式PID算法的计算公式如下： △u(k)=Kp△e(k)+Kie(k)+Kd[△e(k)-△e(k-1)] △e(k)=e(k)–e(k-1) △e(k-1)=e(k-1)–e(k-2) e(k)=r(k)–c(k) 其中，Kp是比例系数，Ki是积分系数，Kd是微分系数，r(k)是期望速度给定值，c(k)是实际速度输出值，e(k)是当前采样时刻的偏差，而△e(k)和△e(k-1)分别表示当前和前一次采样的偏差变化量。通过不断更新这些变量，增量式PID能够动态调整控制量以接近设定值。 在实际应用中，PID参数的整定是一个关键步骤，需要根据系统的特性和控制要求进行调试。通常，这包括了阶跃响应分析、Ziegler-Nichols法则、自适应控制或其他高级优化算法。FPGA由于其灵活性和并行处理能力，成为实现高效、实时PID控制的理想平台，允许快速原型设计和定制化控制算法。 PID控制是自动化和控制系统中的基石，其基本原理和实现方法已经深入人心。无论是在传统的工业设备还是现代的智能系统中，PID控制都发挥着至关重要的作用，确保系统能够准确、稳定地达到预定的目标。