MATLAB在高等代数中的应用：初等变换与方程求解

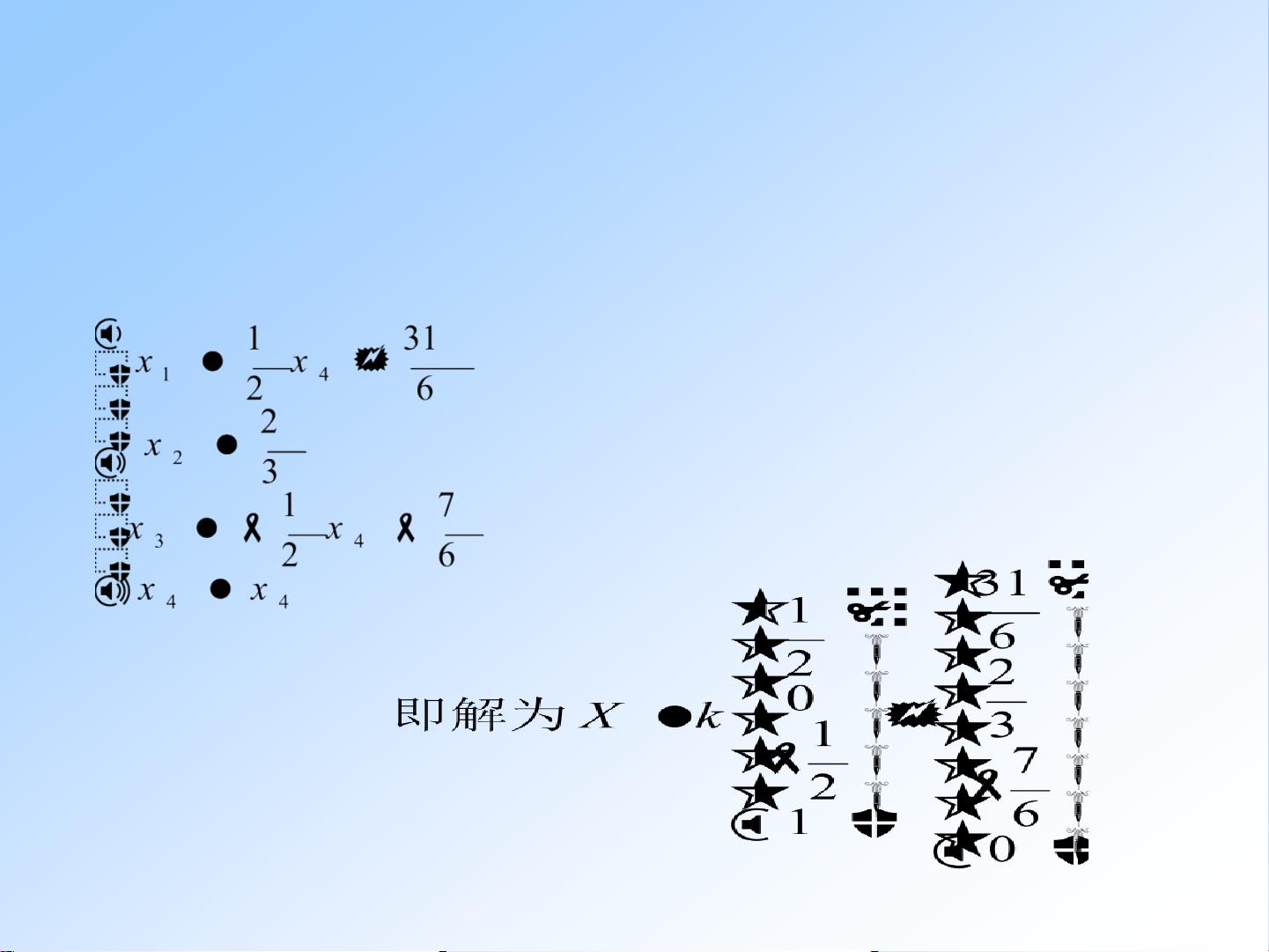
本资源是关于应用MATLAB解决高等代数问题的第四讲内容，主要涵盖了矩阵的初等变换以及线性方程组的求解方法。以下是详细讲解： 1. 矩阵的初等变换： - 该部分介绍了如何在MATLAB中执行基本的矩阵操作，如交换行向量的位置（例如，`A([1,3],:) = A([3,1],:)`），用非零数乘以特定行向量（如`A(2,:) = A(2,:) - A(1,:)*-1`），以及将一个行向量与另一个行向量按需相加（如`A(3,:) = A(3,:) - 3*A(1,:) - 5*A(2,:)`）。 - 使用`formatrat`函数确保计算结果以分数形式展示，以便更准确地表示矩阵操作。 2. 线性方程组的MATLAB求解方法： - 初等变换法：通过一系列的行变换，如上面所述，将矩阵A转换成简化行阶梯形矩阵（`rref(A)`），从而找到线性方程组的解。这里以矩阵`A = [3 -15 3; 1 -12 1; 1 -2 -1]`为例，展示了具体步骤。 - Cramer法则：使用矩阵求逆（`A \ b`）来求解线性方程组，或者通过循环计算系数行列式来逐个求解变量。这种方法对于较小规模的方程组更为直观，但对于大型方程组可能效率较低。 - 矩阵的左除：这是一种直接且常用的求解线性方程组的方法，通过`A \ b`操作得到方程组的解向量`x`。 3. 线性方程组的解结构： - 齐次方程组`AX = 0`的解结构是关键概念，其解空间由所有满足条件的向量构成，这些向量可以看作是原方程组的变量的所有可能组合。 - 解析过程中，通过矩阵的简化形式来描述解的性质，即通过矩阵的秩和自由变量的数量来确定解的结构。 总结来说，本资源是高等代数课程中的一个重要环节，它强调了MATLAB在处理线性代数问题时的实用性和高效性，通过实例演示了如何利用矩阵的初等变换求解线性方程组，并介绍了不同的求解策略。这对于理解和实践数值计算技巧，特别是解决实际问题具有重要意义。