构建赫夫曼树及其应用

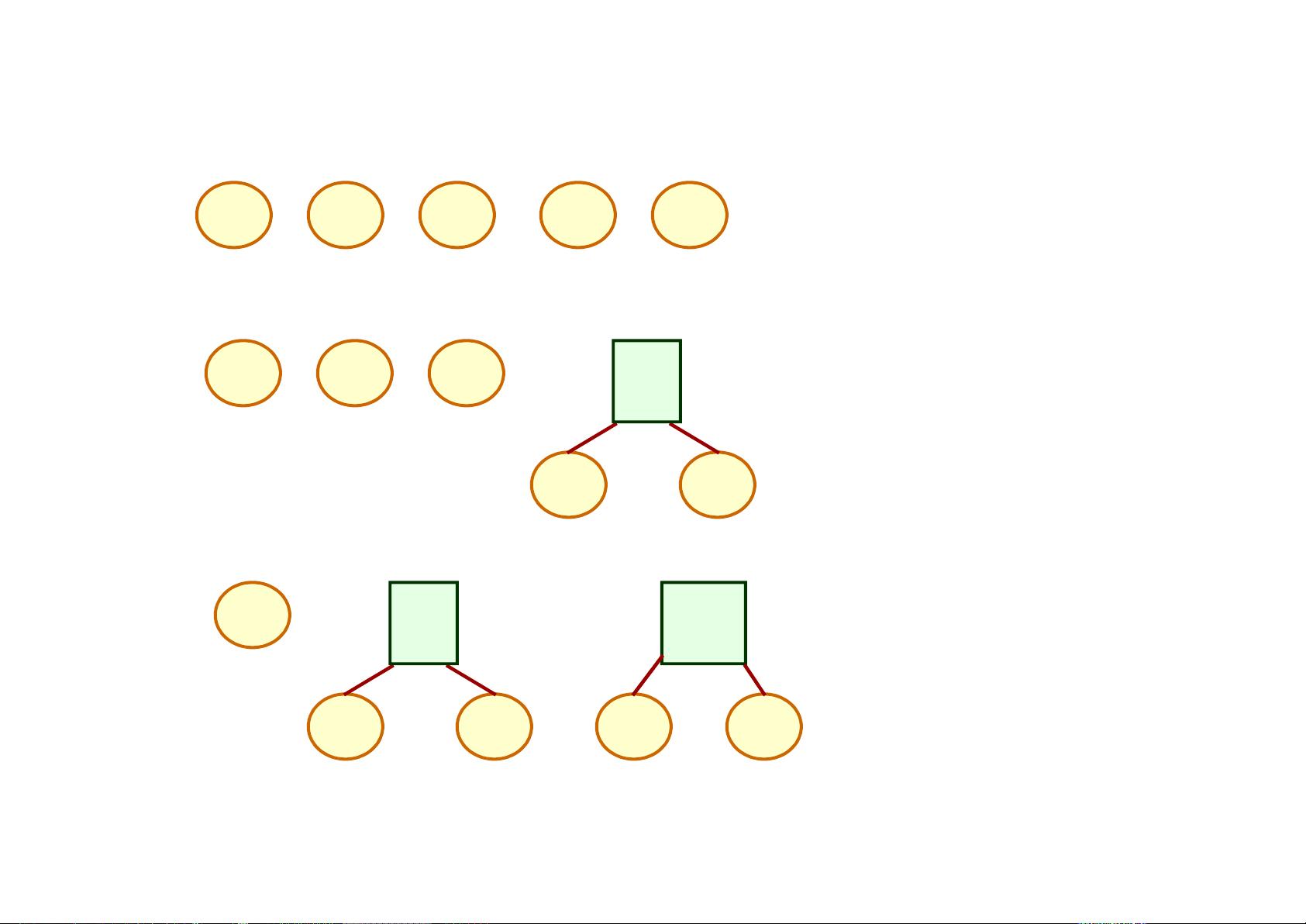
"构建赫夫曼树的算法及应用" 赫夫曼树，也称为最优二叉树，是一种特殊的二叉树结构，它在数据压缩、文件存储等领域有广泛应用。其核心特点是具有最小的带权路径长度（WPL），即树中所有叶子节点的权值与其到达根节点的路径长度乘积之和最小。这种特性使得赫夫曼树成为一种高效的数据结构，尤其在需要频繁访问某些权值较高的数据时。 构造赫夫曼树的过程通常采用赫夫曼算法，这是一个逐步合并小权值节点来构建大树的过程。以下是详细的构造步骤： 1. **初始化**：给定n个权值{w1, w2, ..., wn}，为每个权值创建一个仅包含该权值的单节点二叉树，构成一个集合F，包含n棵树。 2. **合并最小节点**：在集合F中选择权值最小的两棵树，将它们合并为一棵新树，新树的权值是这两棵树的权值之和。新树的左子树是权值较小的原树，右子树是权值次小的原树。 3. **更新集合**：从集合F中移除原来的两棵树，将新生成的树添加到集合F中。 4. **重复步骤2和3**：不断执行上述合并操作，直到集合F中只剩下一棵树为止，这棵树就是赫夫曼树。 为了存储赫夫曼树，通常使用一个数组或链表结构，利用2n-1个元素来表示n个节点，因为赫夫曼树是一个完全二叉树，除了最后一个层次外，其他层次都是满的，且最后一个层次的所有节点都尽可能地靠左排列。 赫夫曼树不仅可以用来构造最小带权路径长度的树，还可以用于生成赫夫曼编码。赫夫曼编码是一种变长编码方式，频率高的字符对应较短的编码，频率低的字符对应较长的编码，这样在传输数据时可以减少平均码长，提高传输效率。具体做法是为每个叶子节点分配唯一的路径，从根节点到叶子节点的路径上的左分支代表0，右分支代表1，这样就得到了每个字符的赫夫曼编码。 在实际应用中，赫夫曼树和编码广泛应用于数据压缩，例如在LZ77、LZ78等压缩算法中，以及在网络通信中的高效传输。此外，赫夫曼树还可以用于解决优先队列问题，例如在Dijkstra最短路径算法中作为优先队列的数据结构。 总结来说，赫夫曼树是一种优化数据存储和传输的工具，通过构造最小带权路径长度的二叉树实现数据的高效处理。它的构造算法和编码方法是计算机科学中的基础概念，对于理解和优化数据处理流程至关重要。