电子科技大学应用随机过程研究生试题解析

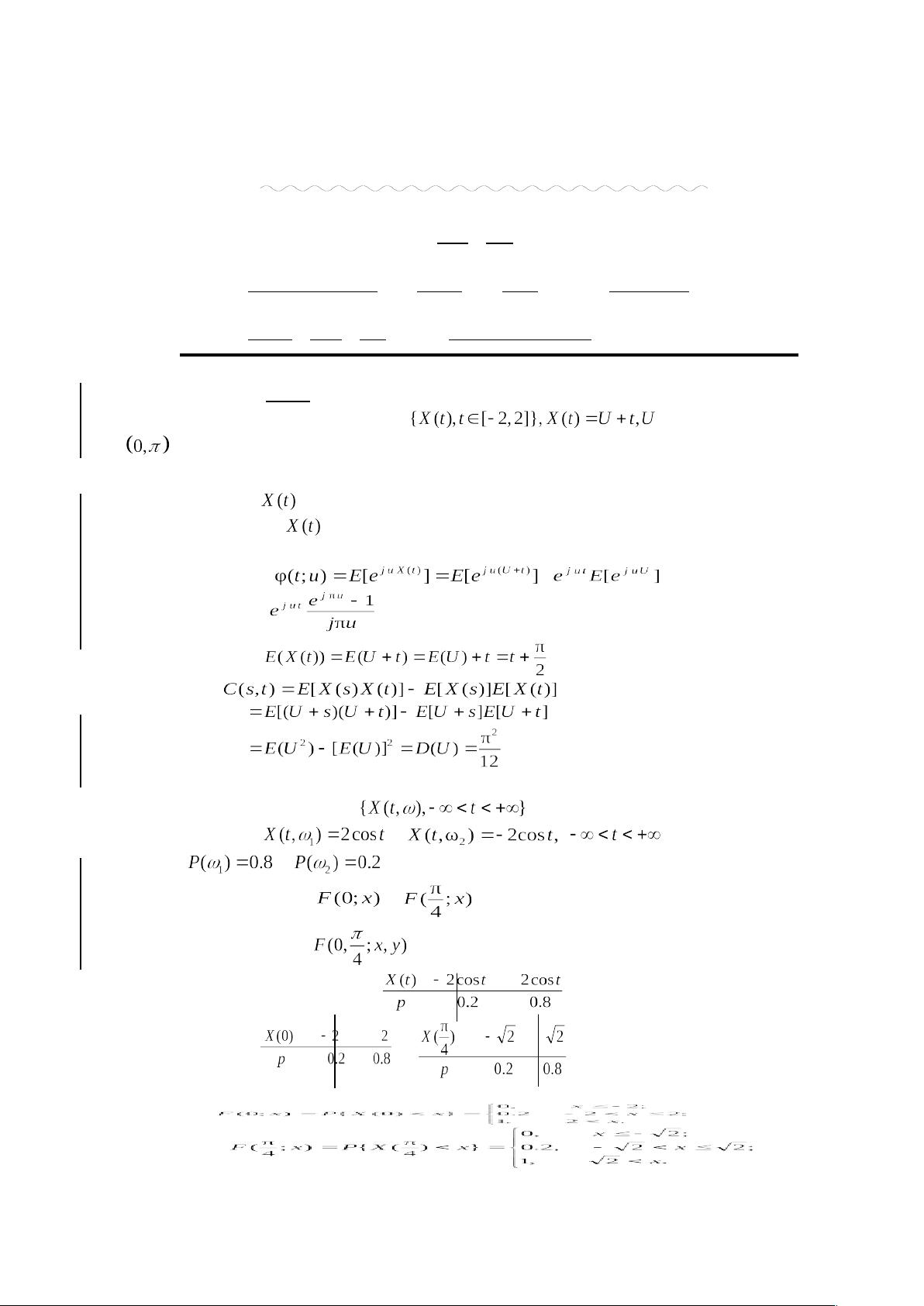
"电子科技大学09应用随机过程试题" 这篇文档是电子科技大学2009年研究生入学考试的应用随机过程试题。试题包含了六个大问题，涵盖了随机过程中的多个核心概念，如样本函数、特征函数、均值函数、自协方差函数、分布函数、泊松过程、指数分布以及宽平稳随机过程等。以下是这些知识点的详细说明： 1. **样本函数**：在随机过程中，样本函数是随机过程在特定时间点或时间段内的可能取值路径。问题一要求绘制样本函数并理解其特性。 2. **特征函数**：特征函数是概率密度函数的傅里叶变换，它包含了随机变量的所有统计信息。问题一中要求求解随机过程的特征函数。 3. **均值函数与自协方差函数**：均值函数是随机过程在每个时间点上的期望值，而自协方差函数则描述了随机过程在不同时间点上的关联性。这些问题中，学生被要求计算这些函数以理解过程的统计性质。 4. **一维与二维分布函数**：一维分布函数给出了随机变量在任意值上的概率，而二维分布函数描述了两个随机变量同时发生的概率。问题二中涉及到了这些函数的计算。 5. **泊松过程**：泊松过程是一种随机过程，其中事件发生的时间点是独立且均匀分布的。问题四中，求解了在一定时间区间内特定数量事件发生的概率以及事件之间的平均间隔。 6. **指数分布**：指数分布常用来描述连续随机变量，例如等待时间。在问题四中，相邻乘客到达的间隔时间就是指数分布的一个实例。 7. **宽平稳随机过程**：如果一个随机过程的均值函数不随时间平移改变，且自相关函数仅依赖于时间差，那么这个过程被称为宽平稳。问题五涉及到了自相关函数和宽平稳过程的概念。 8. **均方导数过程**：在问题五中，均方导数过程与平稳性的关系被讨论，这涉及到随机过程的微分性质。 这些题目反映了应用随机过程课程的主要学习内容，包括随机变量的性质、随机过程的统计特性、以及如何分析和理解随机过程的行为。解答这些问题需要深入理解概率论和随机过程的基本理论，并能够灵活运用这些理论解决实际问题。