SVM优化算法SMO详解与实现

"本文详细介绍了支持向量机（SVM）的优化算法——序列最小最优化（SMO）的实现步骤，并给出了相关定理、证明以及伪代码。" 在机器学习领域，支持向量机（Support Vector Machine，SVM）是一种广泛应用的监督学习模型，尤其在分类和回归任务中表现优异。SMO算法是解决SVM优化问题的一种有效方法，由John Platt提出，用于求解SVM的对偶问题。本文将深入探讨SMO算法的实施过程及其数学证明。 首先，SVM的基本目标是找到一个能够最大化类别间隔的超平面。当数据线性可分时，这个超平面可以将两类样本分开，同时使得两类样本到该超平面的距离最大化。这个距离被称为间隔，而最大化间隔可以提高模型的泛化能力。 SVM的原始问题通常转化为求解其对偶形式，涉及到拉格朗日乘子和KKT条件。对偶问题的形式如下： (2-a) 最小化：\( \sum_{i=1}^{n}\alpha_i - \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jK(x_i,x_j) \) (2-b) 约束条件：\( \alpha_i \geq 0, \quad \forall i \in [1, n] \) (2-c) KKT条件：\( y_i(w^Tx_i - b) = 1, \quad \forall i \in [1, n] \) 这里的\( \alpha_i \)是拉格朗日乘子，\( y_i \)是第i个样本的标签，\( K(x_i,x_j) \)是核函数，\( x_i \)是特征向量，\( w \)是权重向量，\( b \)是偏置项，\( C \)是惩罚参数，\( ξ_i \)是余量，表示样本到决策边界的距离。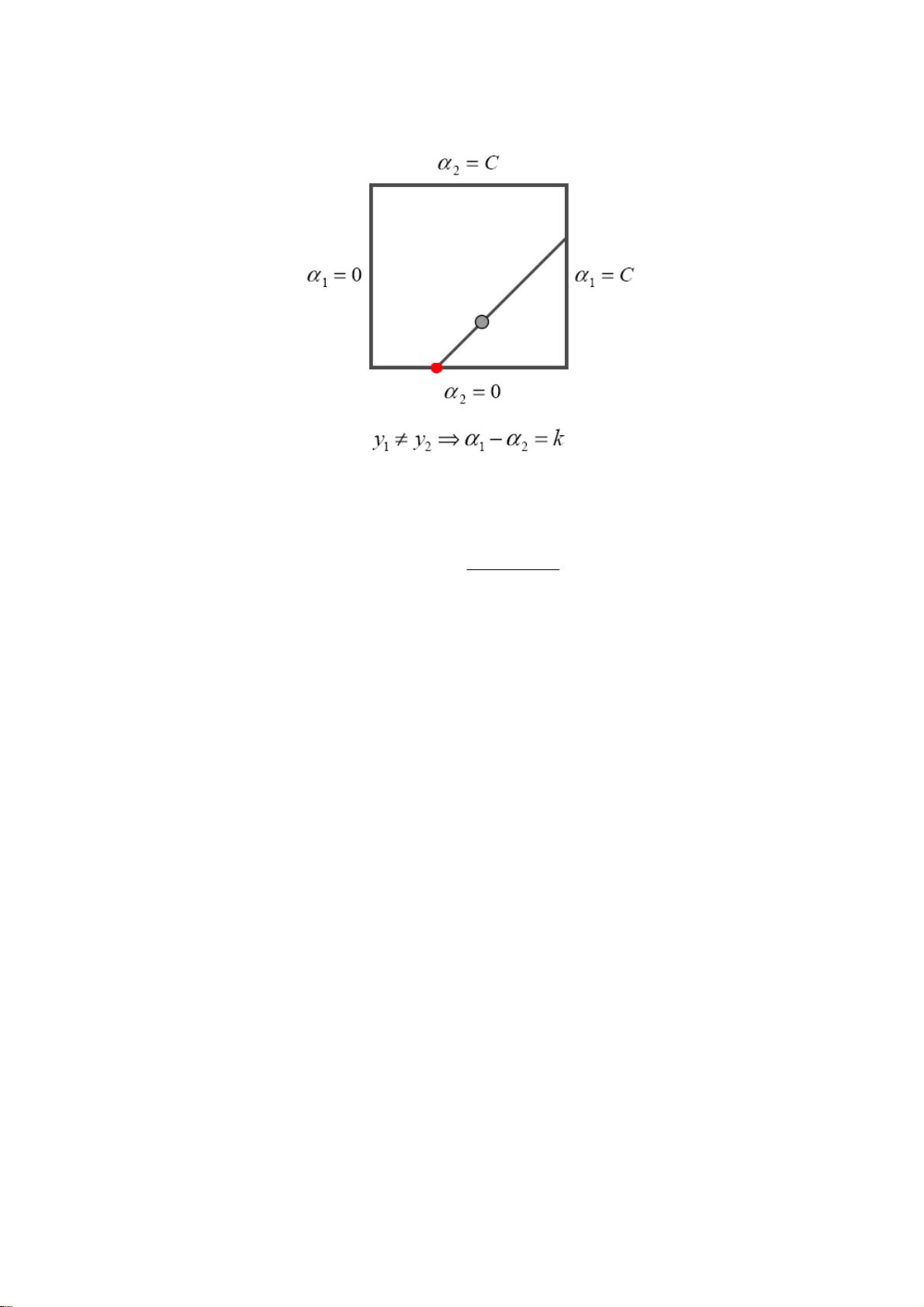 SMO算法的核心是每次选取一对拉格朗日乘子\( \alpha_i \)和\( \alpha_j \)进行优化，同时保持其他\( \alpha_k \)不变。算法的迭代过程如下： 1. 选择一对违反KKT条件的\( \alpha_i \)和\( \alpha_j \)。 2. 更新\( \alpha_i \)和\( \alpha_j \)，保证它们满足KKT条件和约束。 3. 如果新的\( \alpha \)值满足约束，更新权重向量\( w \)和偏置项\( b \)。 4. 检查是否所有\( \alpha \)都满足KKT条件，如果不满足，则返回步骤1，否则算法结束。 SMO算法的伪代码如下： ``` for i=1 to max_iterations do Choose violating pair (i, j) and calculate Ei, Ej If no violating pair exists, break the loop Calculate L, H for α_j using equations Solve for η in the Karush-Kuhn-Tucker conditions Update α_j using L and H If α_j changed, update α_i accordingly Update w and b end for ``` SMO算法通过交替优化一对\( \alpha \)值，有效地解决了SVM的对偶问题，实现了快速收敛，从而提高了SVM的训练效率。通过引入核函数，SVM可以处理非线性可分的数据，将其映射到高维空间，使得原本在原始空间难以分离的样本在高维空间中变得线性可分。 总结来说，SMO算法是SVM的一种高效优化策略，它通过迭代更新拉格朗日乘子来找到最优的分类边界，同时考虑了间隔最大化和样本分布，从而实现了良好的泛化性能。在实际应用中，SMO算法被广泛用于训练大规模数据集的SVM模型。