Matlab模拟正多边形零件摆线加工误差分析

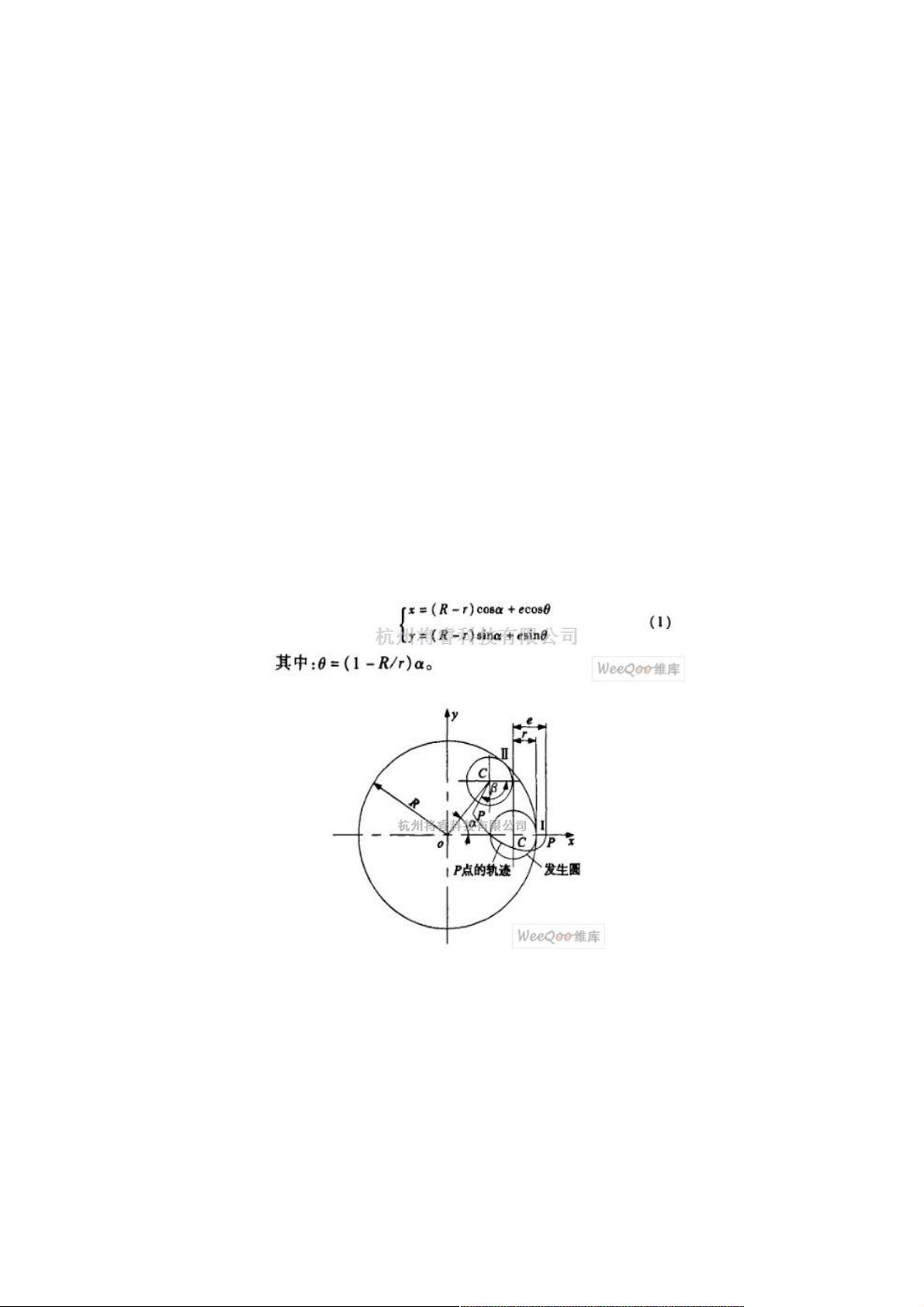
"基于Matlab的正多边形零件连续加工的误差分析" 本文主要探讨了在机械制造领域中，如何利用Matlab软件进行正多边形零件的高效、精确加工，特别是通过摆线原理来优化加工过程。正多边形零件在实际生产中常见，传统加工方法如铣床和刨床的加工工艺往往复杂且效率低下，因为它们涉及到非连续运动，如间隙分度和空行程。摆线原理的应用为解决这一问题提供了新的思路，它能减少所需的运动数量，并保持加工过程的连续性，从而提高加工效率。 Matlab作为一款强大的数值计算和可视化工具，具备数值分析、矩阵运算、信号处理和图形显示等功能，能够简化问题求解的过程。在Matlab环境中，用户可以便捷地输入数学表达式，快速得到数值或图形结果。本文中，作者利用Matlab深入分析了摆线方程中的参数对摆线形状的影响，以及这些参数如何决定摆线对直线的逼近效果和误差分布。 摆线的数学定义是由一个动圆在与之相切的定圆上无滑动滚动时，动圆上固定点的轨迹。其中，基圆和发生圆是摆线形成的关键，基圆半径为R，发生圆半径为r，e为P点到发生圆圆心的距离。通过迭代运算，文章研究了不同参数下摆线的形成，特别是R与r的比例对摆线形状的改变，以及这些变化如何影响加工精度。 此外，文章还计算了满足特定加工精度所需的最小e值，即刀具的最大回转半径，同时考虑了给定最大回转半径下的误差值。这些计算验证了摆线原理在加工正多边形零件时的实用性和可行性。通过对多边形零件的计算分析，可以调整加工参数以优化加工过程，减小误差，确保零件的几何精度。 在实际应用中，理解摆线参数对加工误差的影响至关重要，这有助于制定更精确的加工策略，减少废品率，提高生产效率。通过对Matlab的运用，工程师和研究人员可以更直观地理解摆线原理，优化加工工艺，实现高精度的正多边形零件制造。