【数学游戏】：圆周率计算的趣味性与实用性深度分析


# 摘要
圆周率π作为数学中的一个基础常数，其历史与计算方法吸引了无数数学家和科学家的探索。本文首先概述了圆周率的历史和意义，随后详细介绍了圆周率的计算方法，从古代的几何法和代数法到现代的数值分析法，并探讨了计算技术的革新如何极大地提高了圆周率的计算精度。文章接着转向圆周率的趣味性和教育意义，说明了如何通过游戏和创新教学方法将圆周率知识推广给更广泛的受众。最后，本文分析了圆周率在多个实用领域中的应用，包括科学计算、金融服务以及艺术与设计，展示了圆周率在现代世界的多维价值。

# 关键字
圆周率；计算方法；数值分析；教育意义；科学计算；金融服务

参考资源链接：[MATLAB实现圆周率计算：从刘徽割圆法到数值方法](https://wenku.csdn.net/doc/l2aw30l9wz?spm=1055.2635.3001.10343)
# 1. 圆周率的历史与意义

圆周率（π），一个数学中无处不在的常数，几乎在每一个科学和工程计算中都有其身影。从古至今，它不仅是一个重要的数学概念，也成为了人类文明发展和科技进步的标志。

## 1.1 圆周率的起源
圆周率的概念最早可以追溯到古巴比伦人和古埃及人，他们在土地测量和天文学的实践中发现圆形的周长与直径之间存在着一个固定比率。这个比率被古希腊数学家阿基米德进一步精确，他在使用内接和外切多边形逼近圆的过程中，计算出圆周率的近似值介于3.1408和3.1429之间。

## 1.2 圆周率的文化意义
圆周率在数学之外，还拥有丰富的文化意义。它成为了很多数学爱好者和科学家追求的极限，无数人试图记忆更多的圆周率小数点后的数字，这种追求也成为了科学精神的象征。在文学作品、电影和流行文化中，圆周率也经常被提及，成为了连接科学与大众文化的桥梁。

圆周率的历史和意义，不仅证明了数学概念可以超越时间和空间，还能激励人们在探索未知领域时保持好奇心和创新精神。本章将深入探讨圆周率的发展历程和它在现代社会中的重要性。

# 2. 圆周率的计算方法

## 2.1 传统几何法和代数法

### 2.1.1 阿基米德方法的原理

阿基米德通过使用正多边形逼近圆的周长的方法来计算圆周率，这一方法是古代计算圆周率的经典方法之一。阿基米德使用了正六边形开始，并逐步加倍边数，最终逼近圆的周长。

假设圆的半径为r，那么初始的正六边形周长是3*2*r。
每次边数加倍，新的边长是上一次边长的一半。
随着边数趋于无穷，多边形的周长逼近圆的周长2πr。

通过计算多边形与圆的周长比例，阿基米德推算出圆周率的近似值介于223/71和22/7之间，尽管这个范围并不精确，但该方法奠定了几何逼近法的基础，并被后世广泛应用于圆周率的计算。

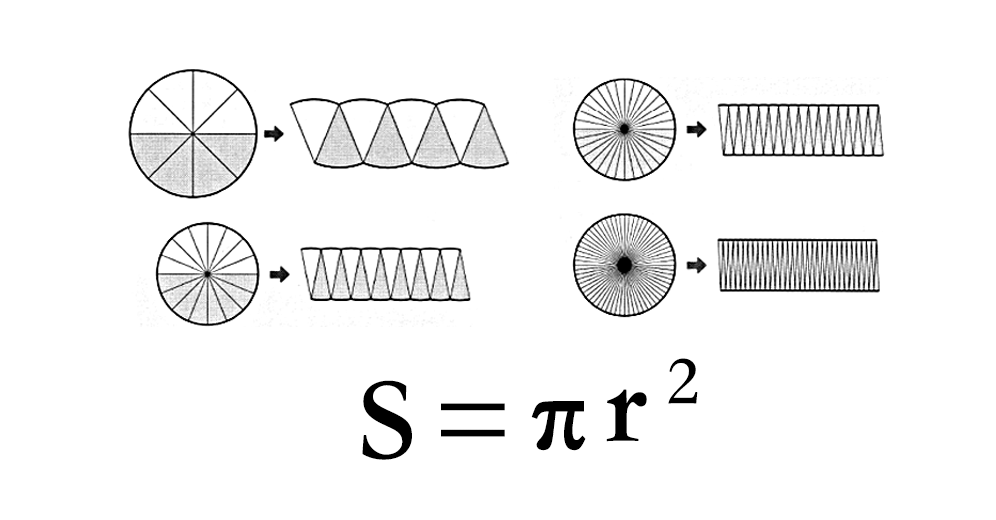
### 2.1.2 中国古代的割圆术

中国古代数学家祖冲之提出的割圆术是一种基于圆内接正多边形逼近计算圆周率的方法。祖冲之计算出圆周率的近似值在3.1415926到3.1415927之间，领先世界近一千年。

割圆术通过反复计算圆内接多边形的周长，不断地增加边数来逼近圆周率。割圆术的基本步骤如下：

- 首先画一个圆，并标记圆心。
- 从圆心出发，每隔一定角度画一条半径到圆周。
- 计算内接多边形的周长，使用勾股定理计算出每一边的长度。
- 不断增加边数，通过几何变换得到更精确的圆周率近似值。

割圆术不仅计算了圆周率的数值，还给出了圆周率的上下界，即约率和密率，分别是22/7和355/113。

## 2.2 现代数值分析法

### 2.2.1 迭代算法的原理和应用

迭代算法是一种重要的数值分析方法，用于求解复杂的数学问题，包括圆周率的计算。迭代算法的原理是通过一系列的近似解逼近最终的准确解。

一个常见的迭代算法是蒙特卡洛方法。蒙特卡洛方法模拟随机过程来估算数值，例如圆周率可以通过随机点的分布来估计。其基本步骤如下：

- 画一个正方形，并在正方形内部画一个内切圆。
- 在正方形内部随机投点，记录落在圆内的点数和总点数。
- 圆面积与正方形面积的比值近似等于圆周率的四分之一。
- 使用公式 π = 4 * (圆内点数 / 总点数)计算圆周率。

这种方法不需要复杂的数学运算，只需通过统计分析即可估算圆周率，非常适合于计算机编程实现。

### 2.2.2 多项式近似与误差分析

在圆周率的计算中，多项式近似是一种通过多项式方程逼近 π 值的方法。例如，泰勒级数可以用来展开 π 的近似值。

泰勒级数近似法的一个经典例子是格雷戈里-莱布尼茨级数：

π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...

使用泰勒级数展开 π 的优点是编程实现简单，但缺点是收敛速度慢，需要计算很多项才能得到较为精确的值。

误差分析是数值分析中的重要部分，特别是对于像 π 这样的无理数。误差分析中涉及到绝对误差和相对误差：

- 绝对误差：真实值与近似值之间的差值。
- 相对误差：绝对误差与真实值的比值。

通过误差分析，可以评估近似方法的准确性和可行性。

### 2.2.3 高斯-勒让德算法深入解析

高斯-勒让德算法是计算圆周率的一种高效算法，它基于连分数的原理。该算法比传统的蒙特卡洛方法收敛更快，适合于需要高精度 π 值的计算。

算法的基本思想是利用连分数的迭代来逼近 π 的值。高斯-勒让德算法的一般步骤如下：

- 将 π 表示为连分数的形式。
- 通过递归迭代求解连分数的分母和分子。
- 每次迭代都逐步接近 π 的真实值。

由于连分数的收敛性质，该算法在较少的迭代次数内就能得到相当精确的 π 值。一个改进的连分数展开如下：

π =