游戏中的异或门与全加器：最简结构解析

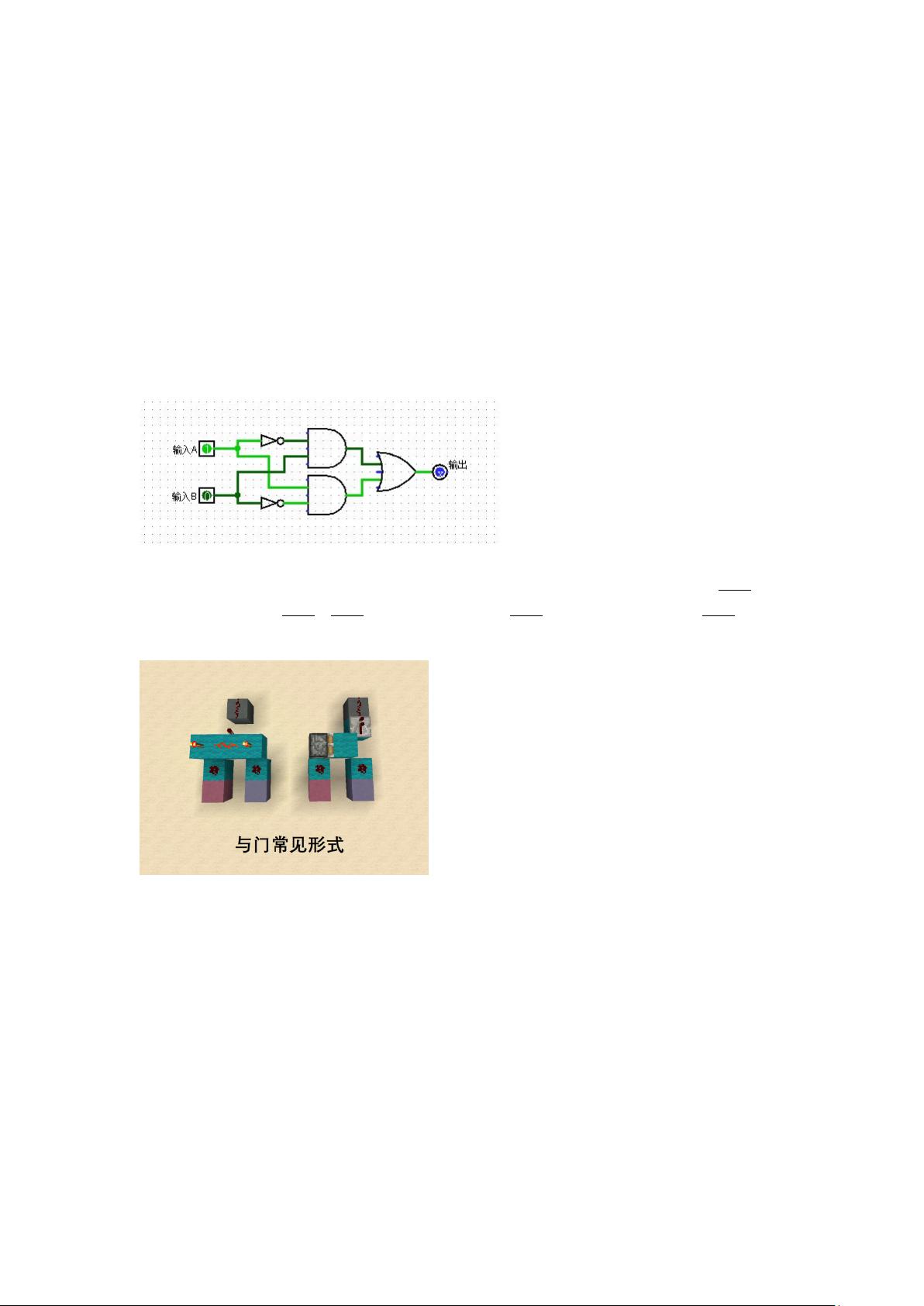
"异或门和全加器最简结构设计原理1" 在电子工程和计算机科学领域，异或门（XOR gate）是一种基本的数字逻辑门，它产生一个输出，该输出是输入信号之间的“互斥”或“排他或”。简单来说，如果输入中的两个比特位相同，输出为0；如果它们不同，输出为1。异或门的逻辑关系可以用以下公式表示： 表达式1：A⊕B = A·B' + B·A' 这里的'表示非操作，·表示与操作，+表示或操作。然而，在某些特定场景，如游戏环境，构建异或门时需要考虑实际可用的逻辑门类型以及电路的物理空间限制。例如，如果与门不是基础逻辑门，需要通过其他门组合实现，那么使用较少的逻辑门就显得尤为重要。 描述中提到了几种可能的异或门表达式，并对它们进行了分析，以找到在游戏环境中更节省空间的实现方式： 表达式2：A⊕B = (A·B)'·A + (A·B)'·B 表达式3：A⊕B = (((A·B)'·A)'·((A·B)'·B)')' 表达式4：A⊕B = (A'+A·B)' + (B'+A·B)' 表达式5：A⊕B = (A·B+A'·B')' 通过逻辑代数的等价变换，可以证明这些表达式与表达式1是等效的。例如，表达式4和5可以通过分配律、德摩根定律等逻辑规则简化为A·B' + B·A'，与表达式1一致。 对于游戏环境中的电路构建，表达式2和3由于包含三个或更多的与门或与非门，可能会导致较大的电路体积，因此不太适合。而表达式4的优势在于，其中的两个A·B可以共用一个与门的输出，从而减少了门的数量。表达式5虽然也使用了两个与门，但通过巧妙利用粘性活塞的特性，可以构造出紧凑的双与门结构，而A'·B'可以视为一个或非门的等效。 在电路设计中，寻找“最简结构”是指找到实现相同逻辑功能但物理结构最小的电路布局。即使是基于相同的逻辑表达式，不同的最简结构可能在输入输出的方向、电路的平面布局或立体尺寸上有所不同。在教学存档中通常会展示几种不同的最简异或门实现，供学习者理解和比较。 全加器是异或门应用的一个重要场景，它是在计算二进制数相加时需要用到的电路单元，能处理进位。全加器不仅包括异或门，还包含与门，用于处理当前位和进位位的逻辑关系。在一个全加器中，两个输入位和一个进位位进行运算，产生一个和位和一个新的进位位。全加器的设计同样需要考虑最简结构，以减少所需的逻辑门数量和电路体积。 异或门和全加器的最简结构设计是数字逻辑和电路设计中的关键问题，尤其是在资源有限的环境下，如游戏中的电路构建。通过深入理解逻辑门的运作和逻辑代数，我们可以找出在物理限制下最有效的电路实现方法。