局部线性嵌入：机器学习中的流形降维方法

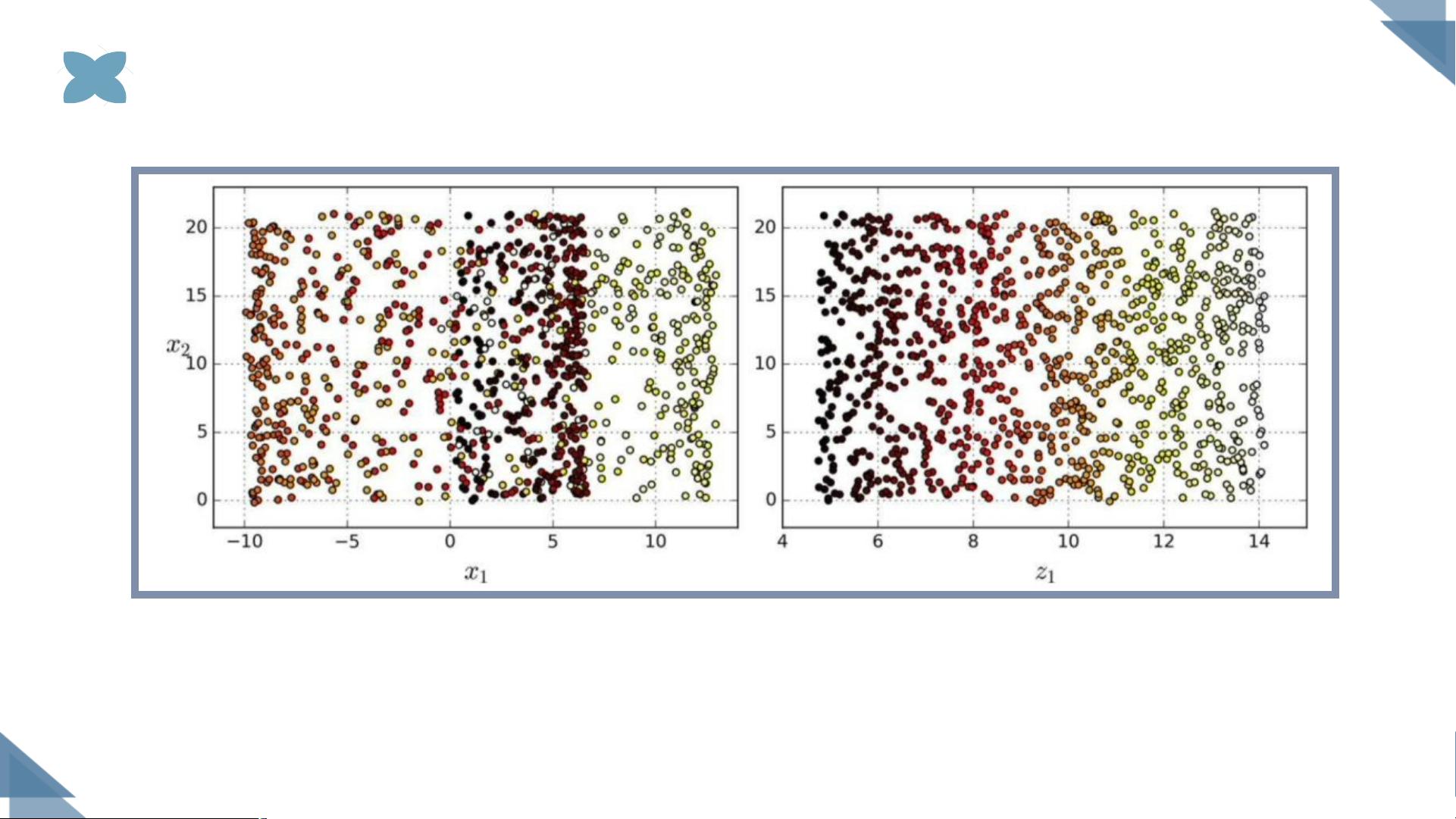
"该资源是关于机器学习中局部嵌入式方法的介绍，特别是局部线性嵌入（Locally-Linear Embedding, LLE）算法。文档提到了高维数据在欧氏空间中的局限性，以及如何通过流形学习来解决非线性数据的处理问题。流形学习的目标是从高维数据中恢复低维流形结构，如PCA、LLE、Laplacian Eigenmaps等算法。其中，LLE算法假设数据在局部范围内是线性的，并且在降维后保持其与近邻点的关系不变。文档还展示了LLE算法的优化问题求解过程以及在瑞士卷数据集上的应用效果，对比了不同近邻数量对降维结果的影响。" 在机器学习领域，局部嵌入式方法是一种处理非线性数据的有效手段。高维数据往往不能简单地用欧式空间的度量来分析，因为真实世界的数据常常存在于复杂的流形结构中。局部线性嵌入（LLE）就是一种流行的流形学习技术，它假设在数据集的局部区域，数据点之间的关系可以用线性模型来近似。LLE的核心思想是找到一个低维空间，使得高维数据在这个低维空间中保持其原有的局部线性结构。 LLE算法首先确定每个数据点的k近邻，然后根据这些近邻构建局部重建权值矩阵。这个矩阵反映了数据点与其近邻之间的线性关系，即假设在降维之后，数据点仍能被其近邻以相同的权重线性表示。接着，LLE通过求解优化问题来寻找低维表示，使得这些局部关系在低维空间中得以保留。 在实践中，LLE的性能受到近邻选择和降维维度的影响。文档中展示了不同近邻数量（如k=10, 5, 30, 50）对瑞士卷数据集降维结果的影响，这表明合适的k值对于保留数据的结构至关重要。同时，LLE与其他流形学习方法如Isomap进行对比，展示了它们在处理特定数据集时的差异。 局部线性嵌入是机器学习中处理非线性数据的重要工具，它通过保留数据的局部线性结构来进行有效的维数约简和数据可视化。理解和掌握LLE算法及其应用场景对于深入理解复杂数据的内在结构以及在实际问题中应用机器学习技术具有重要意义。