小波分析入门：从哈尔函数到二维小波变换

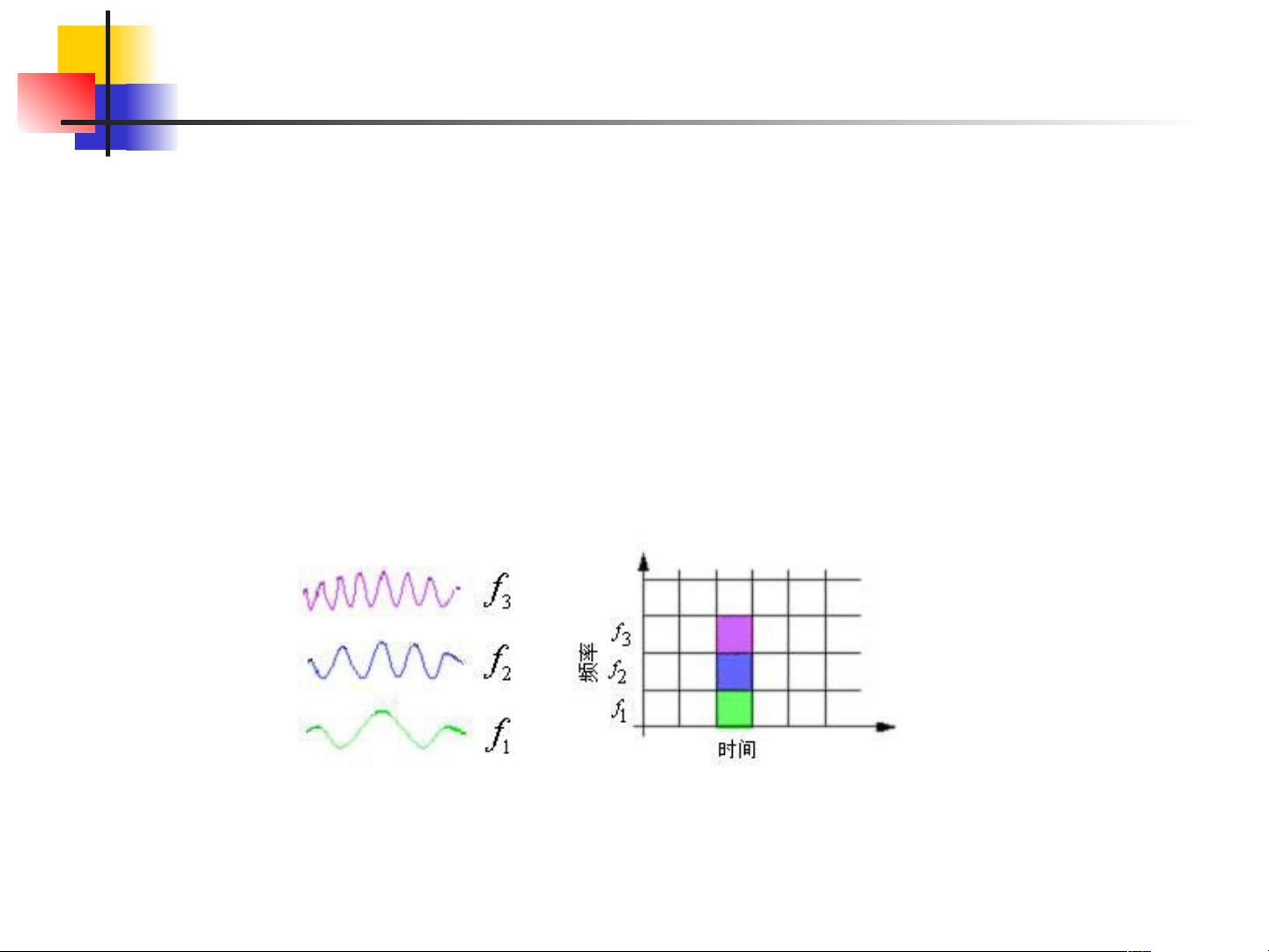
"小波与小波变换.pdf" 小波与小波变换是信号处理和图像分析中的核心概念，尤其在多媒体技术中有着广泛的应用。本讲义由林福宗教授编写，旨在引领读者深入理解小波的世界。小波分析是一种能够同时提供时间和频率信息的分析工具，它弥补了传统傅立叶变换在时间分辨率和频率分辨率上的不足。 小波简史始于1807年，当时Joseph Fourier提出了傅立叶理论，将信号分解为正弦和余弦函数的组合。然而，傅立叶变换虽然能揭示信号的频率成分，但无法精确指示这些频率成分出现的时间。小波变换作为Fourier-Haar-Wavelet Transform的现代发展，提供了更好的时频分析能力。 小波的定义是一个在有限时间内具有零均值的数学函数，它的特性使其在有限的时间和频率范围内具有变化的振幅和频率。部分小波如Moret小波、db6缩放函数和db6小波函数分别由不同的研究者命名并发展。 哈尔函数是小波理论中的一个重要部分，哈尔基函数是一类特殊的小波函数，它们在构造和分析过程中起到关键作用。哈尔小波函数是哈尔基函数的一种形式，通常用于一维信号的分析。通过函数的规范化，可以确保小波函数满足特定的条件，比如正交性或归一化，以便于进行有效的信号分解。 哈尔小波变换是利用哈尔小波函数对信号进行分析的方法，它允许我们将信号分解为不同尺度和位置的局部特征。这种变换可以揭示信号在不同时间尺度上的结构，对于信号压缩、噪声去除以及异常检测等任务非常有用。 在二维哈尔小波变换中，上述概念被扩展到二维空间，适用于图像分析。二维小波变换可以将图像分解为多个小波系数矩阵，每个矩阵对应不同尺度和方向的信息，这对于图像的压缩、增强和边缘检测等应用至关重要。 规范化算法是小波变换中的一个重要环节，它们确保了变换过程的稳定性和计算效率。这些算法通常涉及小波函数的生成、尺度函数的构造以及逆变换的实现，是小波分析技术得以实际应用的关键。 小波与小波变换是信号处理领域的一种强大工具，它结合了时间域和频率域的信息，提供了更为精细的信号分析能力。在多媒体技术、图像处理、语音识别等多个领域，小波分析都有着不可忽视的作用。通过学习和掌握小波理论，我们可以更好地理解和处理复杂信号，为科学研究和工程应用打开新的可能。