揭秘中心极限定理与大数定律：样本估计总体的统计魔法

中心极限定理是统计学中的核心理论，它解释了当我们从一个总体中抽取样本并计算其均值时，即使总体分布并非正态，样本均值的分布也会逐渐趋近于正态分布的现象。这一定理的重要性在于它简化了数据分析和预测的过程，使得我们可以基于相对较小的样本规模得到关于总体的可靠估计。 1. 定义与原理： - 中心极限定理表明，无论总体的原始分布是什么（如均匀、偏斜或非对称），只要样本足够大（通常至少30个独立观测值），样本均值的分布将趋向于正态分布，即样本均值的分布中心接近总体平均值，且标准误差随着样本量增加而减小。 2. 应用实例： - 民意调查是中心极限定理的一个典型应用。通过抽样调查一小部分人群的观点，我们能对整个社会的倾向做出合理的推测。 - 在生产质量控制中，通过检查少数产品的特性，可以推断整个生产线的性能，比如肯德基沙门氏菌检测的例子。 3. 样本估计总体： - 通过多次随机抽取样本，计算平均值，可以形成一个关于总体的估计。中心极限定理保证了这种估计的精度随着样本数量的增加而提高。 4. 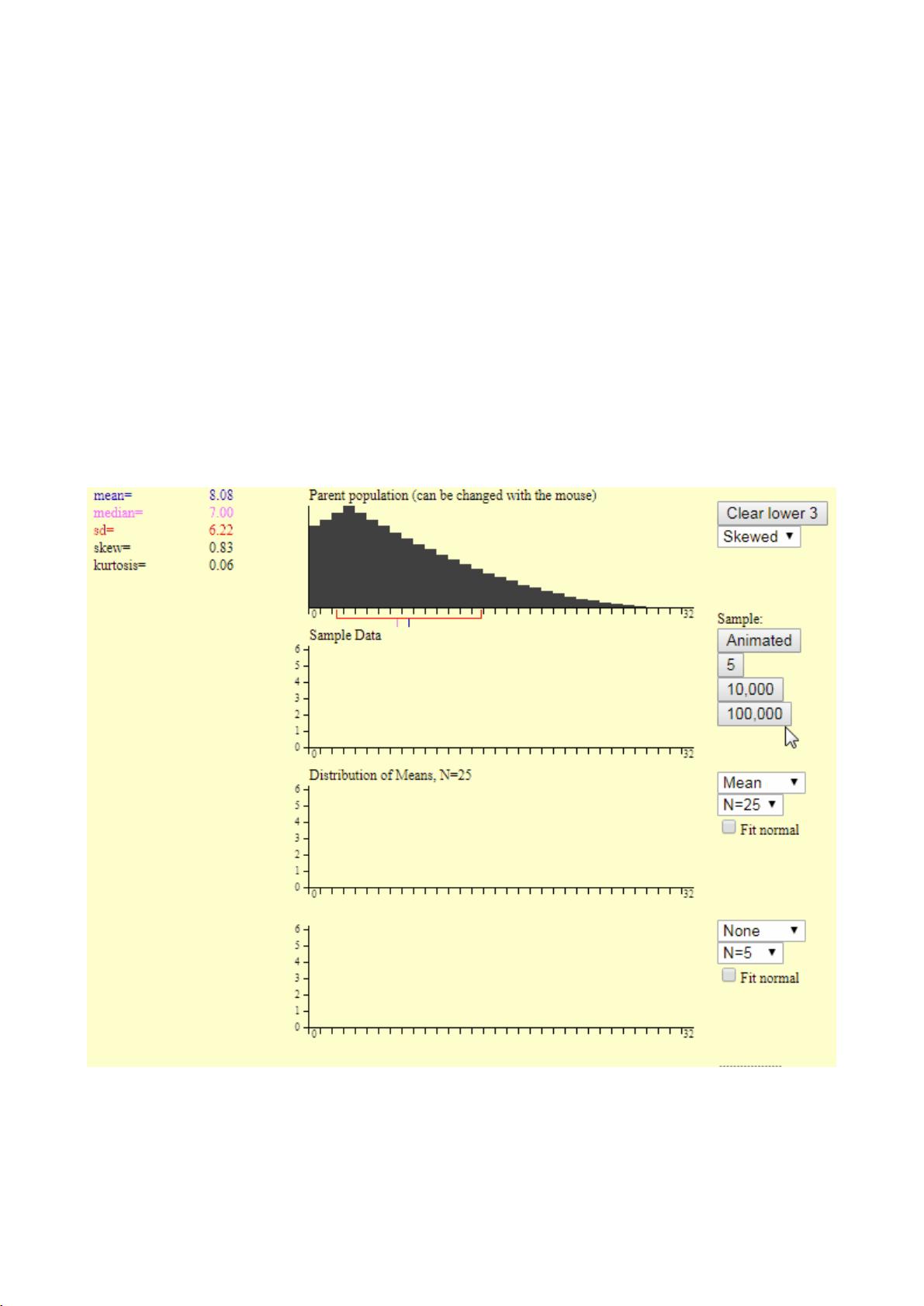计算和可视化： - 小程序演示了中心极限定理的实际操作，用户可以通过模拟不同总体分布和样本大小，观察样本均值分布的变化，直观感受定理的效果。 5. 中心极限定理与大数定律的区别： - 大数定律关注的是单个事件的频率在大量重复试验中趋于稳定，而中心极限定理则关注的是样本均值的分布。两者相辅相成，共同构成了统计分析的基础。 6. 注意事项： - 为了保证中心极限定理的有效性，样本大小至关重要，一般建议至少30个数据点，但实际应用中可能需要根据具体问题调整。 理解中心极限定理对于数据分析人员、统计学家以及决策者来说至关重要，因为它简化了复杂的数据处理过程，使得我们能够在面对大量不确定性时，依赖有限的信息做出可靠的决策。在实际工作中，合理运用中心极限定理可以显著提升统计推断的效率和准确性。