Matlab实现Koch分形及其实验程序

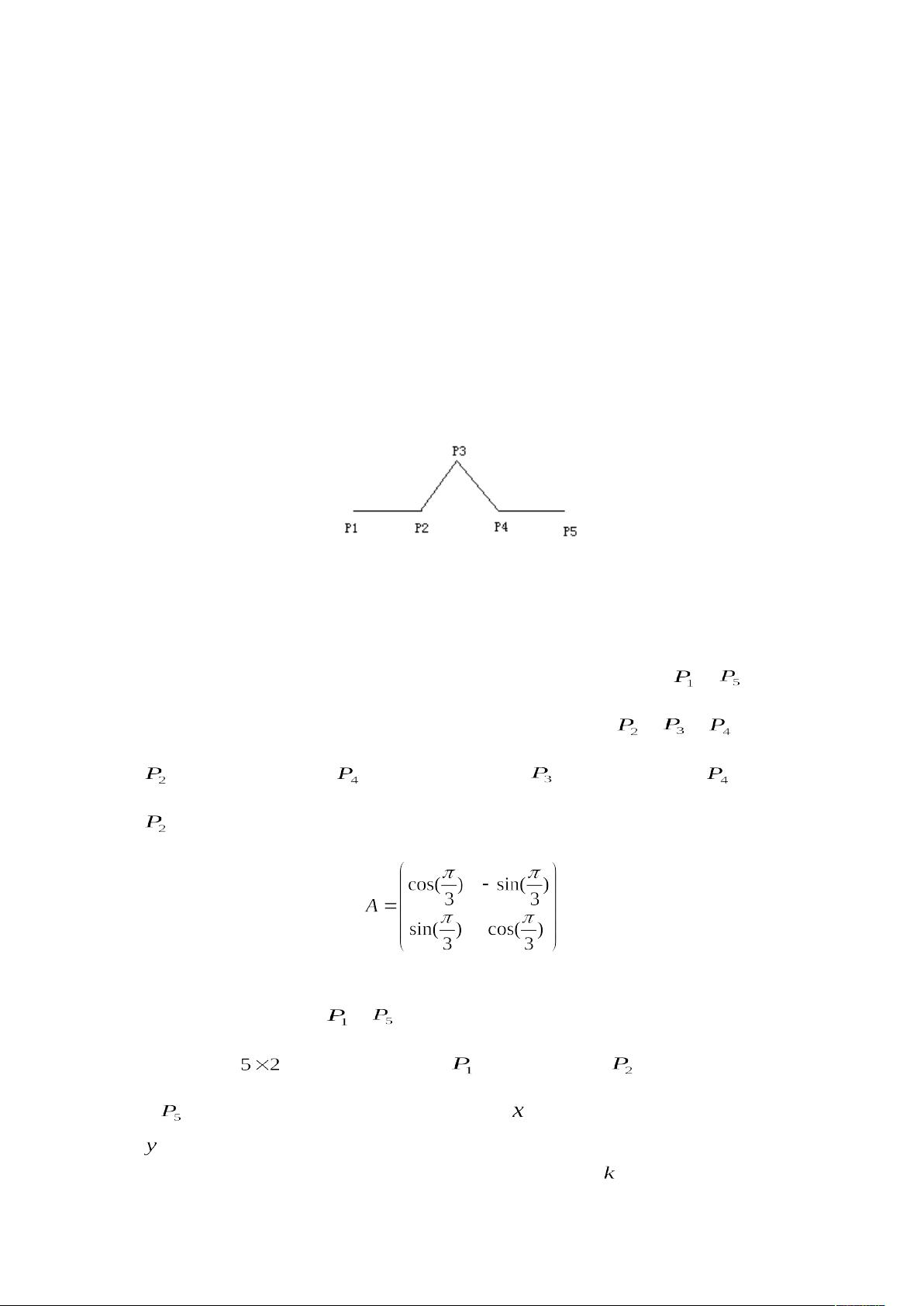
本篇文章主要介绍了如何在MATLAB中实现几个经典的分形图形，特别是Koch分形曲线的生成过程。Koch分形是一种自相似的几何形状，它通过不断迭代和复制简单的图案来创建复杂的无限序列。文章以一种直观的方式展示了分形生成的步骤，从一条直线段开始，每次迭代都将线段的三分之一替换为一个等边三角形，这个过程不断重复，形成著名的Koch曲线。 首先，文章定义了问题的关键步骤：在MATLAB中，设两个端点为[pic]和[pic]，初始直线段被分割成三部分，分别插入三个新的点[pic]、[pic]和[pic]，其中[pic]和[pic]是按照正交矩阵[pic]进行60度旋转得到的。这个过程可以用一个矩阵表示，矩阵中的行代表各个点的坐标，列则对应x和y坐标。 然后，作者讨论了分形结点数的增长规律。对于Koch曲线，每次迭代都会增加结点数，第[pic]次迭代后的结点数比上一次增加了4倍减去3（即[pic]）。这个递推关系确保了分形的自相似性。 在实验部分，作者给出了具体的MATLAB代码示例。初始点[pic]的坐标被存储在变量p中，n表示当前迭代次数，A是旋转矩阵。通过循环迭代，每次迭代中计算相邻点之间的向量，将其长度除以3以适应等边三角形的插入，然后更新点的坐标。通过这种方式，逐步构建起Koch分形曲线。 总结起来，本文详细地讲解了如何利用MATLAB编程实现Koch分形的生成，包括算法原理、节点坐标计算以及迭代过程的实现，为读者提供了一个直观且实用的学习工具，以便更好地理解和欣赏分形的数学之美。通过这个例子，读者可以学习到如何运用编程语言处理几何变换和递归算法来创建自相似结构。