深度学习驱动的高效3D隐式体积与纹理压缩技术

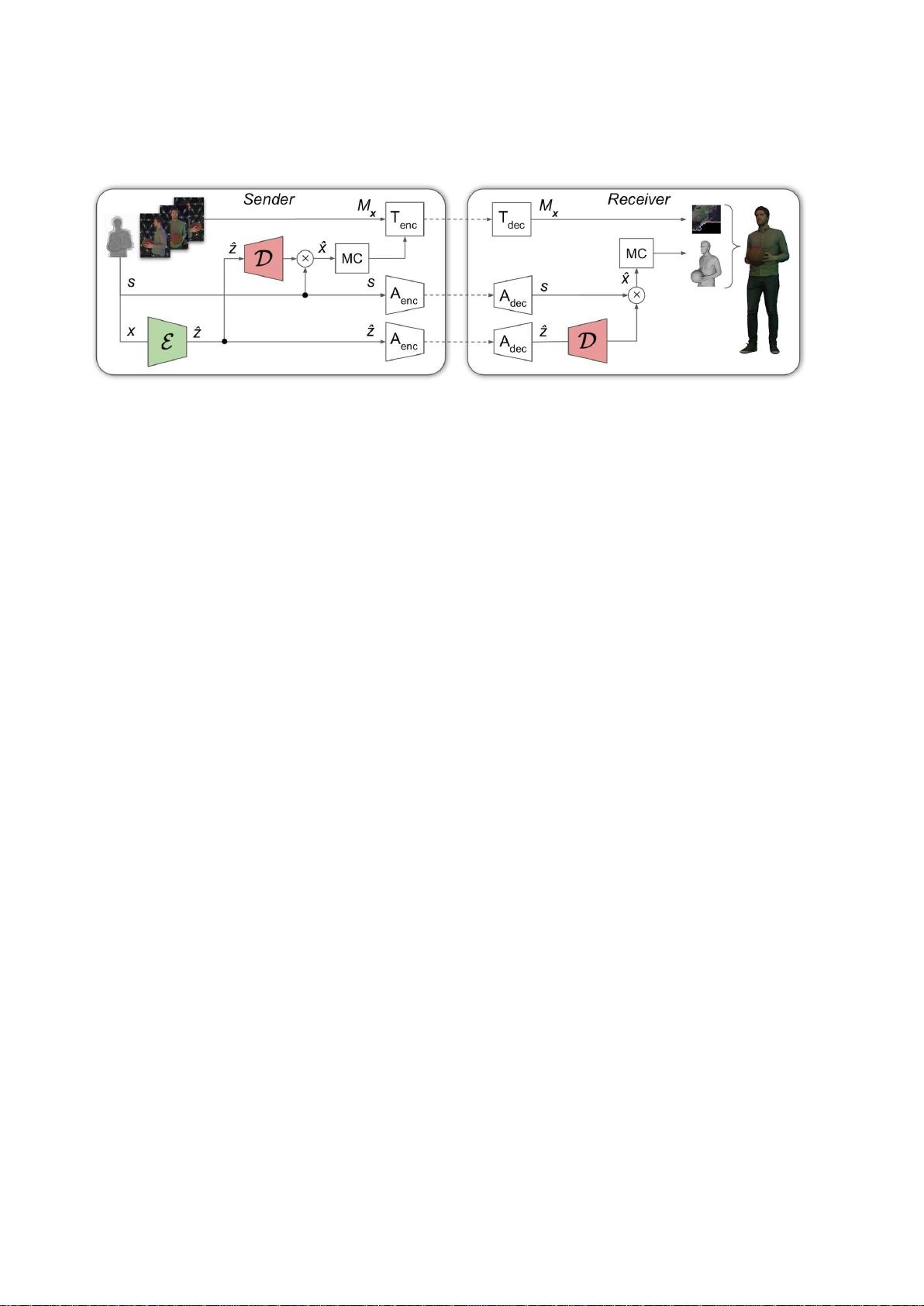
"深度隐式体积压缩及其对应的纹理压缩方法" 深度隐式体积压缩是一种新兴的技术，主要用于优化存储和传输3D体素网格中的截断有符号距离场（TSDF）和相关纹理。TSDF是3D重建领域常用的一种数据结构，它能够表示物体表面附近的密度信息，常用于构建密集表面映射和自由视点视频。然而，这些表示方法往往需要大量的内存空间，特别是在处理高分辨率的4D数据时。 本文由谷歌的研究人员提出，他们设计了一种基于块状神经网络架构的端到端训练方法，用于压缩TSDF。这种方法旨在实现最佳的率失真平衡，即在压缩数据的同时尽可能减少信息丢失，保证重建的质量。为了防止在解压过程中出现拓扑错误，他们无损地压缩TSDF的符号信息，并通过设定体素大小的上界来限制可能的重建误差。 此外，针对与TSDF相关的纹理压缩，研究者们提出了一种快速的基于块状UV参数化的方法。该方法能生成一致的纹理贴图，随后利用现有的视频压缩算法（如H.264或HEVC）进行高效压缩。实验结果显示，他们的算法在两个4D性能捕捉数据集上对比现有最先进的方法，能在保持相同失真水平的情况下降低66%的比特率，或者在相同比特率下减少50%的失真。 论文中引用的前文表明，TSDF由于其体素值的相关性和规则的网格结构，被证明适合高效压缩。而传统的压缩方法如Draco[24]可能需要对低多边形网格进行简化，这可能导致细节丢失，而其他方法可能产生块状伪影（如[59]所示）。相比之下，该研究的新方法在保持低比特率的同时，显著降低了失真。 3D形状学习的编码器-解码器架构，借鉴了图像处理领域的卷积神经网络（CNN）的成功经验，特别适用于处理具有网格结构的数据。因此，研究者可能将这样的深度学习技术应用于压缩过程，以提高效率和重建质量。 这篇论文介绍了一种创新的压缩策略，旨在解决3D和4D数据存储和传输的挑战，特别是对于那些需要高效压缩以适应VR/AR、远程存在感和自由视点视频流的应用。该方法的贡献在于结合了深度学习和传统压缩技术的优势，以达到更高的压缩效率和更优的视觉效果。