首页把一个校长为6dm的正方体钢块造成横截面积为4的方体钢锭,这根钢链长多少分米?
把一个校长为6dm的正方体钢块造成横截面积为4的方体钢锭,这根钢链长多少分米?
时间: 2024-03-30 22:36:44 浏览: 94
首先,我们可以根据正方体的体积公式 $V=a^3$,计算出这个正方体的体积为 $6^3=216$ $dm^3$。然后,我们可以根据题意知道,这个正方体钢块被造成了一个横截面积为 $4$ $dm^2$ 的方体钢锭,因此,它的长度为 $216/4=54$ $dm$。最后,我们需要计算这根钢链的长度,即这个方体钢锭的对角线长度。根据勾股定理,这个方体钢锭的对角线长度为 $\sqrt{a^2 + b^2 + c^2}$,其中 $a$, $b$, $c$ 分别是这个方体的三条棱的长度。由于这个方体是正方体,所以 $a=b=c=54/\sqrt{3}$ $dm$,因此,这个方体钢锭的对角线长度为 $54\sqrt{3}$ $dm$,约等于 $93.53$ $dm$。所以这根钢链的长度约为 $93.53$ $dm$。
阅读全文
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
最新推荐
体育课评分系统 微信小程序+SSM毕业设计 源码+数据库+论文+启动教程.zip
体育课评分系统 微信小程序+SSM毕业设计 源码+数据库+论文+启动教程
项目启动教程:https://www.bilibili.com/video/BV1BfB2YYEnS
JHU荣誉单变量微积分课程教案介绍
资源摘要信息:"jhu2017-18-honors-single-variable-calculus"
知识点一:荣誉单变量微积分课程介绍
本课程为JHU(约翰霍普金斯大学)的荣誉单变量微积分课程,主要针对在2018年秋季和2019年秋季两个学期开设。课程内容涵盖两个学期的微积分知识,包括整合和微分两大部分。该课程采用IBL(Inquiry-Based Learning)格式进行教学,即学生先自行解决问题,然后在学习过程中逐步掌握相关理论知识。
知识点二:IBL教学法
IBL教学法,即问题导向的学习方法,是一种以学生为中心的教学模式。在这种模式下,学生在教师的引导下,通过提出问题、解决问题来获取知识,从而培养学生的自主学习能力和问题解决能力。IBL教学法强调学生的主动参与和探索,教师的角色更多的是引导者和协助者。
知识点三:课程难度及学习方法
课程的第一次迭代主要包含问题,难度较大,学生需要有一定的数学基础和自学能力。第二次迭代则在第一次的基础上增加了更多的理论和解释,难度相对降低,更适合学生理解和学习。这种设计旨在帮助学生从实际问题出发,逐步深入理解微积分理论,提高学习效率。
知识点四:课程先决条件及学习建议
课程的先决条件为预演算,即在进入课程之前需要掌握一定的演算知识和技能。建议在使用这些笔记之前,先完成一些基础演算的入门课程,并进行一些数学证明的练习。这样可以更好地理解和掌握课程内容,提高学习效果。
知识点五:TeX格式文件
标签"TeX"意味着该课程的资料是以TeX格式保存和发布的。TeX是一种基于排版语言的格式,广泛应用于学术出版物的排版,特别是在数学、物理学和计算机科学领域。TeX格式的文件可以确保文档内容的准确性和排版的美观性,适合用于编写和分享复杂的科学和技术文档。
管理建模和仿真的文件
管理Boualem Benatallah引用此版本:布阿利姆·贝纳塔拉。管理建模和仿真。约瑟夫-傅立叶大学-格勒诺布尔第一大学,1996年。法语。NNT:电话:00345357HAL ID:电话:00345357https://theses.hal.science/tel-003453572008年12月9日提交HAL是一个多学科的开放存取档案馆,用于存放和传播科学研究论文,无论它们是否被公开。论文可以来自法国或国外的教学和研究机构,也可以来自公共或私人研究中心。L’archive ouverte pluridisciplinaire
【实战篇:自定义损失函数】:构建独特损失函数解决特定问题,优化模型性能
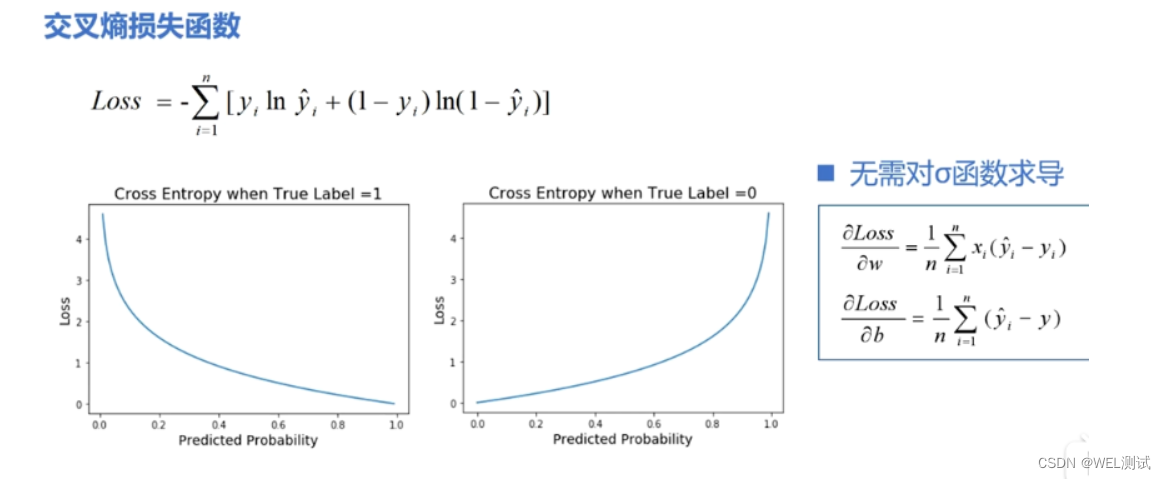
# 1. 损失函数的基本概念与作用
## 1.1 损失函数定义
损失函数是机器学习中的核心概念,用于衡量模型预测值与实际值之间的差异。它是优化算法调整模型参数以最小化的目标函数。
```math
L(y, f(x)) = \sum_{i=1}^{N} L_i(y_i, f(x_i))
```
其中,`L`表示损失函数,`y`为实际值,`f(x)`为模型预测值,`N`为样本数量,`L_i`为第`i`个样本的损失。
## 1.2 损
如何在ZYNQMP平台上配置TUSB1210 USB接口芯片以实现Host模式,并确保与Linux内核的兼容性?
要在ZYNQMP平台上实现TUSB1210 USB接口芯片的Host模式功能,并确保与Linux内核的兼容性,首先需要在硬件层面完成TUSB1210与ZYNQMP芯片的正确连接,保证USB2.0和USB3.0之间的硬件电路设计符合ZYNQMP的要求。
参考资源链接:[ZYNQMP USB主机模式实现与测试(TUSB1210)](https://wenku.csdn.net/doc/6nneek7zxw?spm=1055.2569.3001.10343)
具体步骤包括:
1. 在Vivado中设计硬件电路,配置USB接口相关的Bank502和Bank505引脚,同时确保USB时钟的正确配置。
Naruto爱好者必备CLI测试应用
资源摘要信息:"Are-you-a-Naruto-Fan:CLI测验应用程序,用于检查Naruto狂热者的知识"
该应用程序是一个基于命令行界面(CLI)的测验工具,设计用于测试用户对日本动漫《火影忍者》(Naruto)的知识水平。《火影忍者》是由岸本齐史创作的一部广受欢迎的漫画系列,后被改编成同名电视动画,并衍生出一系列相关的产品和文化现象。该动漫讲述了主角漩涡鸣人从忍者学校开始的成长故事,直到成为木叶隐村的领袖,期间包含了忍者文化、战斗、忍术、友情和忍者世界的政治斗争等元素。
这个测验应用程序的开发主要使用了JavaScript语言。JavaScript是一种广泛应用于前端开发的编程语言,它允许网页具有交互性,同时也可以在服务器端运行(如Node.js环境)。在这个CLI应用程序中,JavaScript被用来处理用户的输入,生成问题,并根据用户的回答来评估其对《火影忍者》的知识水平。
开发这样的测验应用程序可能涉及到以下知识点和技术:
1. **命令行界面(CLI)开发:** CLI应用程序是指用户通过命令行或终端与之交互的软件。在Web开发中,Node.js提供了一个运行JavaScript的环境,使得开发者可以使用JavaScript语言来创建服务器端应用程序和工具,包括CLI应用程序。CLI应用程序通常涉及到使用诸如 commander.js 或 yargs 等库来解析命令行参数和选项。
2. **JavaScript基础:** 开发CLI应用程序需要对JavaScript语言有扎实的理解,包括数据类型、函数、对象、数组、事件循环、异步编程等。
3. **知识库构建:** 测验应用程序的核心是其问题库,它包含了与《火影忍者》相关的各种问题。开发人员需要设计和构建这个知识库,并确保问题的多样性和覆盖面。
4. **逻辑和流程控制:** 在应用程序中,需要编写逻辑来控制测验的流程,比如问题的随机出现、计时器、计分机制以及结束时的反馈。
5. **用户界面(UI)交互:** 尽管是CLI,用户界面仍然重要。开发者需要确保用户体验流畅,这包括清晰的问题呈现、简洁的指令和友好的输出格式。
6. **模块化和封装:** 开发过程中应当遵循模块化原则,将不同的功能分隔开来,以便于管理和维护。例如,可以将问题生成器、计分器和用户输入处理器等封装成独立的模块。
7. **单元测试和调试:** 测验应用程序在发布前需要经过严格的测试和调试。使用如Mocha或Jest这样的JavaScript测试框架可以编写单元测试,并通过控制台输出调试信息来排除故障。
8. **部署和分发:** 最后,开发完成的应用程序需要被打包和分发。如果是基于Node.js的应用程序,常见的做法是将其打包为可执行文件(如使用electron或pkg工具),以便在不同的操作系统上运行。
根据提供的文件信息,虽然具体细节有限,但可以推测该应用程序可能采用了上述技术点。用户通过点击提供的链接,可能将被引导到一个网页或直接下载CLI应用程序的可执行文件,从而开始进行《火影忍者》的知识测验。通过这个测验,用户不仅能享受答题的乐趣,还可以加深对《火影忍者》的理解和认识。
"互动学习:行动中的多样性与论文攻读经历"
多样性她- 事实上SCI NCES你的时间表ECOLEDO C Tora SC和NCESPOUR l’Ingén学习互动,互动学习以行动为中心的强化学习学会互动,互动学习,以行动为中心的强化学习计算机科学博士论文于2021年9月28日在Villeneuve d'Asq公开支持马修·瑟林评审团主席法布里斯·勒菲弗尔阿维尼翁大学教授论文指导奥利维尔·皮耶昆谷歌研究教授:智囊团论文联合主任菲利普·普雷教授,大学。里尔/CRISTAL/因里亚报告员奥利维耶·西格德索邦大学报告员卢多维奇·德诺耶教授,Facebook /索邦大学审查员越南圣迈IMT Atlantic高级讲师邀请弗洛里安·斯特鲁布博士,Deepmind对于那些及时看到自己错误的人...3谢谢你首先,我要感谢我的两位博士生导师Olivier和Philippe。奥利维尔,"站在巨人的肩膀上"这句话对你来说完全有意义了。从科学上讲,你知道在这篇论文的(许多)错误中,你是我可以依
【强化学习损失函数探索】:奖励函数与损失函数的深入联系及优化策略
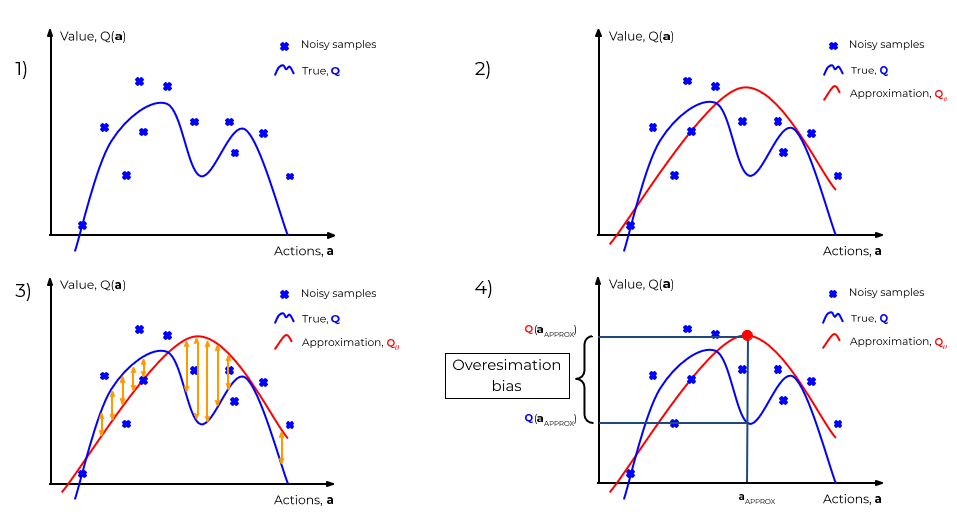
# 1. 强化学习中的损失函数基础
强化学习(Reinforcement Learning, RL)是机器学习领域的一个重要分支,它通过与环境的互动来学习如何在特定任务中做出决策。在强化学习中,损失函数(loss function)起着至关重要的作用,它是学习算法优化的关键所在。损失函数能够衡量智能体(agent)的策略(policy)表现,帮助智能体通过减少损失来改进自
如何在Springboot后端项目中实现前端的多人视频会议功能,并使用Vue.js与ElementUI进行界面开发?
要在Springboot后端项目中实现前端的多人视频会议功能,首先需要了解Springboot、WebRTC、Vue.js以及ElementUI的基本概念和用途。Springboot作为后端框架,负责处理业务逻辑和提供API接口;WebRTC技术则用于实现浏览器端的实时视频和音频通信;Vue.js作为一个轻量级的前端框架,用于构建用户界面;ElementUI提供了丰富的UI组件,可加速前端开发过程。
参考资源链接:[多人视频会议前端项目:Springboot与WebRTC的结合](https://wenku.csdn.net/doc/6jkpejn9x3?spm=1055.2569.3001
Android应用显示Ignaz-Taschner-Gymnasium取消课程概览
资源摘要信息:"Android应用'vertretungsplan-itg-android'是专门为Ignaz-Taschner-Gymnasium的学生设计的,旨在让他们能够快速查看和了解已取消的课程情况。此应用程序具有的关键特征包括提供一个快速概述已取消课程的功能,适合学生在移动中查看,以及自动更新课程信息的能力,以确保显示的是最新数据。开发该应用的编程语言是Java,它是一种广泛使用的通用编程语言,特别适合开发Android应用程序。"
以下是根据标题、描述和标签生成的知识点:
1. Android应用开发:Android应用是基于Linux内核的操作系统,专为移动设备设计。应用的开发涉及到使用Android SDK(软件开发工具包)以及一种或多种编程语言,比如Java。
2. Java编程语言:Java是一种高级、面向对象的编程语言,广泛应用于各种平台的应用程序开发。Android应用开发中,Java提供了丰富的类库和API,方便开发者快速构建应用程序。
3. 应用功能设计:该应用的设计目的是为学生提供一个查看已取消课程的快速方式。快速概述的实现可能是通过简化用户界面和优化数据检索逻辑来完成的。
4. 移动应用的可用性:为了满足学生在路上使用的需求,应用程序可能具有响应式设计,以适应不同屏幕尺寸的设备,并确保内容在各种设备上都能清晰易读。
5. 数据更新机制:自动更新功能意味着应用程序能够在后台定期检查服务器上的新信息,并在有课程变动时及时将最新的课程状态提供给用户,无需用户手动刷新或更新应用。
6. 教育行业应用:这类应用程序通常针对特定的教育机构,提供学生和教职工特定的服务。在这个案例中,应用程序是为Ignaz-Taschner-Gymnasium的学生定制的,它展示了如何利用技术为特定用户提供定制化的解决方案。
7. 项目管理与命名规范:从提供的文件名称"vertretungsplan-itg-android-master"可以推测,该应用程序可能是一个开源项目,"master"表明了这是一个主版本或者主分支,通常包含了最新的稳定代码。
8. 跨平台工具的缺失:尽管存在一些如React Native或Flutter这样的跨平台框架可以用来开发Android和iOS应用,但该项目使用Java进行开发,这可能意味着它是一个专为Android平台设计的应用程序。
9. 用户体验(UX)设计:应用程序的易用性和直观性是用户体验设计的关键组成部分。应用的快速概述和自动更新等功能的实现都需要综合考虑用户体验,以确保学生能够方便快捷地获得所需信息。
10. 应用发布与维护:一旦开发完成,该应用程序需要通过Google Play Store或其他Android应用市场发布,并且需要定期更新和维护以修复可能存在的bug和提升用户体验。
综上所述,该Android应用不仅满足了特定用户群体的需求,还体现了应用开发过程中的关键考虑因素,如用户体验、数据管理、项目维护以及Java编程语言的运用。