【实战篇：自定义损失函数】：构建独特损失函数解决特定问题，优化模型性能

# 1. 损失函数的基本概念与作用

## 1.1 损失函数定义
损失函数是机器学习中的核心概念，用于衡量模型预测值与实际值之间的差异。它是优化算法调整模型参数以最小化的目标函数。

L(y, f(x)) = \sum_{i=1}^{N} L_i(y_i, f(x_i))

其中，`L`表示损失函数，`y`为实际值，`f(x)`为模型预测值，`N`为样本数量，`L_i`为第`i`个样本的损失。

## 1.2 损失函数的作用
损失函数不仅指导模型学习，还影响模型的泛化能力。选择合适的损失函数对于提高模型性能至关重要。以下是损失函数的三个主要作用：

- **指导学习**：通过最小化损失函数，模型可以学习到数据中的规律。
- **性能度量**：损失函数的值可以作为模型性能的直接评估指标。
- **超参数调整**：损失函数的值常用于选择和调整模型超参数。

# 2. 理论基础与损失函数设计

损失函数在机器学习和深度学习中是不可或缺的，它们是衡量模型预测值和真实值之间差异的函数，指导模型进行优化。本章节将深入探讨损失函数的数学原理，并讨论设计自定义损失函数的必要性和原则。

### 损失函数的数学原理

#### 损失函数的定义

损失函数，也被称作代价函数或误差函数，量化了模型预测的误差。它是模型参数的函数，目标是通过调整参数来最小化损失函数的值。在数学上，损失函数通常表示为：

\[ L(y, \hat{y}) = f(y, \hat{y}) \]

这里，\( y \) 是真实值，而 \( \hat{y} \) 是模型的预测值。函数 \( f \) 表示了损失的计算方法。

#### 常见损失函数的理论分析

常见的损失函数包括均方误差（MSE）、交叉熵（Cross-Entropy）等。例如，均方误差定义为：

\[ MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y_i})^2 \]

其中 \( N \) 是样本数量。MSE 是回归问题中常用的损失函数，它对大误差有更大的惩罚，因为它会将误差平方。

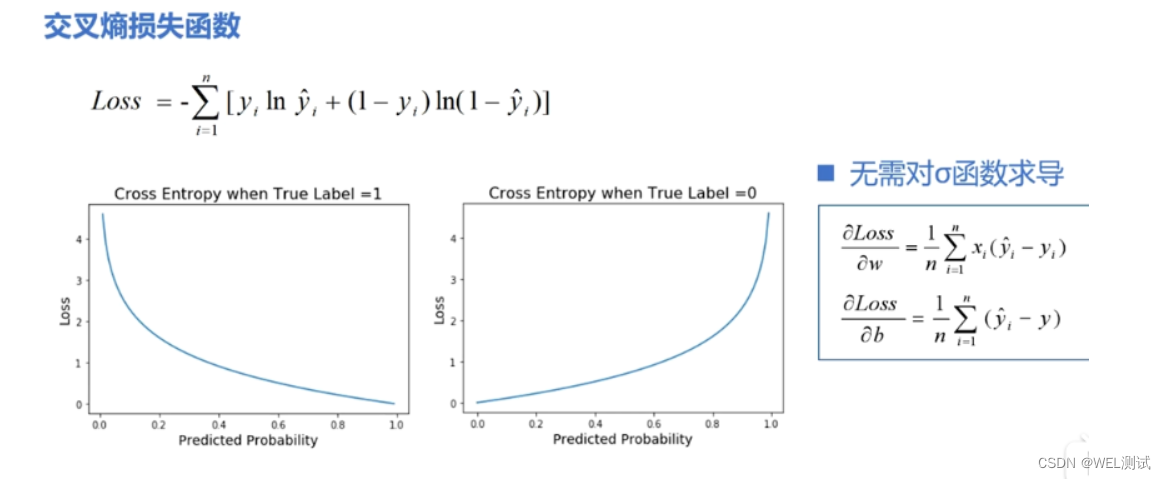
交叉熵损失在分类问题中应用广泛，特别是在多类别分类问题中。其定义为：

\[ CE = - \sum_{c=1}^{M} y_c \log(\hat{y_c}) \]

这里 \( M \) 是类别数量，\( y_c \) 是一个指示变量，如果样本属于类别 \( c \) 则为1，否则为0；\( \hat{y_c} \) 是模型预测样本属于类别 \( c \) 的概率。

### 自定义损失函数的必要性

#### 标准损失函数的局限性

尽管有大量预定义的损失函数，但在某些特定问题上，标准损失函数可能不完全适用。例如，当数据不平衡时，传统的损失函数可能无法公平地评估所有类别，导致模型偏向多数类。

#### 自定义损失函数的优势

自定义损失函数能够更好地反映问题的特定需求。例如，通过调整损失函数以给予某些类型错误更大的权重，可以改善对不平衡数据的分类。

### 设计自定义损失函数的原则

#### 数据分布的考量

在设计损失函数时，必须考虑数据分布的特点。例如，当数据分布具有长尾特性时，可以设计一种损失函数，使得模型对尾部数据的预测误差更加敏感。

#### 问题特点的映射

损失函数的设计应映射问题的本质特征。例如，在时间序列预测问题中，可以设计损失函数以反映时间连续性，比如通过时间相关的误差惩罚项来强化模型对时间相关性的学习。

通过下一章节的深入讨论，我们将了解如何结合具体的机器学习问题特征来设计并实现自定义损失函数，以及如何结合优化算法来提升自定义损失函数的有效性。

# 3. 自定义损失函数实践方法

## 3.1 基于问题特征的损失函数设计

### 3.1.1 非对称损失函数的构建

在许多实际应用中，数据集中的类别可能并不平衡，例如，某些类别的样本数量远多于其他类别。在这些情况下，标准的对称损失函数可能会导致模型对多数类别过度拟合，而忽视了少数类别，从而降低了模型的泛化能力。为了处理这种类别不平衡问题，我们可以设计非对称损失函数，赋予不同类别不同的权重，以纠正类别不平衡带来的影响。

非对称损失函数的关键在于为每个类别定义不同的损失权重。举例来说，对于二分类问题，我们可以定义以下的非对称损失函数：

def asymmetric_loss(y_true, y_pred, class_weights):
    """
    非对称损失函数的实现。
    :param y_true: 真实标签向量。
    :param y_pred: 模型预测的概率。
    :param class_weights: 类别权重向量，针对不同类别有不同的权重。
    :return: 计算出的损失值。
    """
    # 计算交叉熵损失，并根据类别权重进行调整
    loss = - (y_true * np.log(y_pred) * class_weights[0] +
              (1 - y_true) * np.log(1 - y_pred) * class_weights[1])
    return loss.mean()

# 假设类别权重为 [0.5, 2.0]，即少数类别的权重是多数类别的四倍
weights = np.array([0.5, 2.0])

在上述代码中，`y_true` 是包含真实标签的数组，`y_pred` 是模型预测的概率，`class_weights` 是一个包含两个元素的数组，分别代表正类和负类的权重。根据实际情况，我们可以对类别权重进行调整以达到最佳效果。

### 3.1.2 组合损失函数的实现

组合损失函数是将两个或多个不同的损失函数结合起来以获得更好的性能。这种方法特别适合于复杂任务，比如同时考虑预测的准确性和输出的置信度。一个典型的例子是在目标检测中，我们可能同时希望优化边界框的定位准确性和分类的准确性。

组合损失函数的一般形式可以是：

def combined_loss(y_true, y_pred, loss_functions, weights):
    """
    组合损失函数的实现。
    :param y_true: 真实标签向量。
    :param y_pred: 模型预测的输出。
    :param loss_functions: 单个损失函数的列表。
    :param weights: 相应损失函数的权重。
    :return: 计算出的组合损失值。
    """
    combined_loss = 0
    for loss_function, weight in zip(loss_functions, weights):
        # 计算每个损失函数的值并累加，每个损失函数都有一个权重
        combined_loss += loss_function(y_true, y_pred) * weight
    return combined_loss

# 假设我们结合交叉熵和均方误差
loss_functions = [keras.losses.categorical_crossentropy, keras.losses.mean_squared_error]
weights = [0.7, 0.3]  # 权重的总和必须为1

在实际应用中，我们需要根据具体问题来选择和调整损失函数及其权重，以达到最佳的模型性能。

## 3.2 结合优化算法的损失函数实现

### 3.2.1 梯度下降法的适配

梯度下降法是一种常用的优化算法，用于求解损失函数的最小值。在自定义损失函数时，必须确保损失函数可微，以便梯度下降法能够计算出损失函数相对于模型参数的梯度，从而更新参数以降低损失值。

def gradient_descent(model, loss_function, X, y, learning_rate=0.01, epochs=100):
    """
    使用梯度下降法适配自定义损失函数。
    :param model: 模型对象。
    :param loss_function: 自定义损失函数。
    :param X: 特征数据集。
    :param y: 标签数据集。
    :param learning_rate: 学习率。
    :param epochs: 迭代次数。
    """
    for epoch in range(epochs):
        # 前向传播计算损失
        predictions = model(X)
        loss = loss_function(y, predictions)
        # 计算损失函数相对于模型参数的梯度
        gradients = tape.gradient(loss, model.trainable_variables)
        # 更新模型参数
        optimizer.apply_gradients(zip(gradients, model.trainable_variables))
        if epoch % 10 == 0:
            print(f'Epoch {epoch}, Loss: {loss.numpy()}')

在上述代码中，`tape` 是 TensorFlow 中用于自动微分的工具，`optimizer` 是优化器对象。

### 3.2.2 高级优化技术的集成

随着深度学习技术的发展，梯度下降法的许多变体，如动量梯度下降、Adagrad、RMSprop 和 Adam，也被广泛应用于各种问题中。这些高级优化技术引入了额外的机制来加速收敛并提高模型的性能。

以 Adam 优化器为例，它结合了动量梯度下降和 RMSprop 的思想，能够自适应地调整每个参数的学习率。在 Keras 中使用 Adam 优化器可以非常简单：

model = ...  # 创建模型
model.compile(