卷积神经网络的数学计算公式

卷积神经网络（Convolutional Neural Network，CNN）是一种前馈神经网络，它通常应用于图像识别、语音识别等领域。其数学计算公式如下：

1. 卷积层
假设输入的是一个大小为 W1 × H1 × D1 的数据，卷积核的大小为 F × F，步长为 S，填充为 P，那么卷积后输出的大小为 W2 × H2 × D2，其中：

W2 = (W1 - F + 2P) / S + 1
H2 = (H1 - F + 2P) / S + 1
D2 = K

其中 K 表示卷积核的数量。

2. 池化层
假设输入的是一个大小为 W1 × H1 × D1 的数据，池化窗口的大小为 F × F，步长为 S，那么池化后输出的大小为 W2 × H2 × D1，其中：

W2 = (W1 - F) / S + 1
H2 = (H1 - F) / S + 1

3. 全连接层
假设输入的是一个大小为 N 的向量，全连接层共有 M 个神经元，则输出的大小为 M。

以上是卷积神经网络中常用的数学计算公式，具体的实现还需要结合具体的框架和实现方式来确定。

相关问题

卷积神经网络的数学公式

C#卷积神经网络（Convolutional Neural Network，CNN）是一种常用于图像识别计算机视觉任务的深度学习模型。它通过使用卷积层、池化层和全连接层等组件来提取图像特征并进行分类。

数学公式在描述CNN时起到了重要的作用。下面是CNN中几个关键概念的数学公式：

1. 卷积操作：
在CNN中，卷积操作用于提取图像的局部特征。假设输入图像为X，卷积核为W，那么卷积操作可以表示为：
其中，* 表示卷积操作，Y 是输出特征图。

2. 激活函数：
在卷积层或全连接层后，通常会应用一个非线性激活函数来引入非线性变换。常见的激活函数有ReLU、Sigmoid和Tanh等。以ReLU函数为例，其数学公式为：

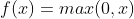
3. 池化操作：
池化操作用于降低特征图的空间维度，并保留重要的特征。常见的池化操作有最大池化和平均池化。以最大池化为例，其数学公式为：

4. Softmax函数：
在CNN中用于多分类问题时，通常会使用Softmax函数将网络输出转换为概率分布。Softmax函数可以表示为：
其中，S_i 是第 i 个类别的概率，X_i 是网络输出的第 i 个元素。

这些是CNN中一些常见的数学公式，它们在实现卷积神经网络时起到了关键作用。

卷积神经网络的数学推导 pdf

### 回答1：
卷积神经网络（Convolutional Neural Network，简称CNN）是一种基于数学推导的深度学习算法，主要用于图像识别和处理。其数学推导包括了卷积运算、非线性激活函数、池化操作等。

在卷积神经网络中，卷积运算是其中一个核心概念。它通过对输入数据和滤波器（也称为卷积核）进行卷积操作，实现对输入数据的特征提取。卷积运算通过在输入数据上滑动滤波器，并将滤波器与输入数据中的对应部分相乘，然后将所有相乘的结果相加。这个过程可以通过数学推导和矩阵运算来实现，通过矩阵的乘法和求和操作，可以高效地进行卷积运算。

非线性激活函数是卷积神经网络中的另一个重要部分。它的作用是在卷积运算的结果上引入非线性变换，从而增加网络的表达能力。常见的非线性激活函数包括ReLU、Sigmoid和Tanh等。这些激活函数通过数学推导和函数的运算，将卷积运算的结果映射到一定范围内，以实现非线性的特征表示。

池化操作是卷积神经网络中的另一个关键步骤。它通过对输入数据进行降采样，减少数据的维度，从而进一步提取图像的特征。常见的池化操作包括最大池化和平均池化。最大池化选择输入数据中的最大值作为输出，而平均池化则取输入数据的均值作为输出。这些操作可以通过数学推导和简单的运算实现。

除了上述推导，卷积神经网络还包括了多层的神经网络结构、损失函数的定义、反向传播算法等。通过这些推导，我们可以更好地理解卷积神经网络的原理和工作原理，为图像处理和识别提供理论基础和数学支持。

### 回答2：
卷积神经网络（Convolutional Neural Network, CNN）是一种主要应用于图像和语音识别等领域的深度学习算法。卷积神经网络的数学推导在一定程度上可以帮助我们理解其工作原理和运行机制。

卷积神经网络的数学推导主要涉及卷积操作和反向传播算法。首先，我们需要了解卷积操作。卷积操作是卷积神经网络中最重要的运算之一，它通常用于提取输入数据的特征。在数学推导中，卷积操作可以通过定义卷积核（或滤波器）和输入数据的卷积来实现。卷积操作的数学推导可以详细解释如何通过卷积核对输入数据进行滤波和特征提取。

另外，数学推导还包括了卷积神经网络的反向传播算法。反向传播算法是用于更新网络参数的关键步骤，通过计算损失函数对网络参数的导数，可以得到参数的梯度并进行参数更新。反向传播算法的数学推导可以详细解释如何计算网络参数的导数，并通过链式法则将梯度从输出层传播到输入层。

卷积神经网络的数学推导是一项复杂和深奥的任务，需要对线性代数、微积分和概率统计等数学知识有一定的了解。在理解和应用卷积神经网络时，对其数学推导的掌握可以提供清晰的思路和直观的认识。同时，掌握卷积神经网络的数学推导还可以帮助我们理解和处理网络中的各个参数和运算过程，进而优化和改进网络的性能。

总而言之，卷积神经网络的数学推导在一定程度上可以帮助我们理解网络的工作原理和运行机制。通过学习卷积操作和反向传播算法的数学推导，我们可以更加清晰地理解卷积神经网络的各个组成部分，为进一步的研究和应用提供基础和指导。

### 回答3：
卷积神经网络（Convolutional Neural Networks, CNN）是一种深度学习模型，特别适用于图像处理任务。其数学推导主要集中在卷积运算和反向传播算法两个方面。

卷积运算是CNN的核心操作，它基于滤波器（Filter）对输入数据进行局部感知和特征提取。假设输入数据为二维矩阵（如图像），滤波器为一个小的二维矩阵，卷积运算通过将滤波器与输入数据的不同位置进行逐元素相乘，然后将结果求和，得到一个输出特征值。通过滑动窗口的方式，可以在整个输入数据上进行卷积运算，得到一个特征图。

在数学上，卷积运算可以表示为：
\[f(i, j) = \sum_{m} \sum_{n} g(m, n) \cdot w(i-m, j-n)\]
其中，\(f(i, j)\)表示输出特征图上的某个位置的值，\(g(m, n)\)表示输入数据上的某个位置的值，\(w(i-m, j-n)\)表示滤波器的权重。这个公式可以看作是对输入数据与滤波器进行一次像素级的逐元素相乘，然后将结果求和得到输出特征图上对应位置的值。

反向传播算法是CNN中的训练算法，用于在已知标签的样本上，通过更新网络参数来最小化损失函数。数学上，反向传播算法主要涉及到对损失函数求导的过程，以确定每一层网络参数的更新方向和大小。

通过链式法则，我们可以将总损失对某一层参数的导数表示为前一层参数的导数与该层输出对该层参数的导数的乘积，这样便可以通过逐层反向传播，计算每一层参数的梯度，并利用梯度下降等优化算法来更新参数。

总结起来，卷积神经网络的数学推导主要包括卷积运算和反向传播算法。卷积运算利用滤波器对输入数据进行特征提取，而反向传播算法则用于训练网络参数。这些数学推导为CNN在图像处理等领域的应用提供了理论基础，并为算法改进和网络设计提供了方向。