【ANSYS Fluent流场可视化】：后处理结果优化技巧大公开


# 摘要
本文全面介绍了ANSYS Fluent在流场可视化领域的应用基础、数据处理理论、后处理技巧以及高级技术探讨。首先概述了ANSYS Fluent流场可视化的基础，然后深入讲解了流场数据处理的理论基础，包括流体动力学基本概念和数据处理技术。接着，详细阐述了ANSYS Fluent后处理的技巧和高级功能，通过案例分析展示了流场可视化在工业和科研领域的实际应用。最后，探讨了实时流场模拟与可视化的高级技术以及大数据在流场数据后处理中的应用。本研究旨在为流体力学研究者和工程师提供一个流场可视化综合指南，从而提高流场分析的准确性和效率。

# 关键字
ANSYS Fluent；流场可视化；流体动力学；数据处理；后处理；实时模拟；大数据分析

参考资源链接：[ANSYS Fluent 2022 R1 官方帮助文档学习指南](https://wenku.csdn.net/doc/7q23hxmfrf?spm=1055.2635.3001.10343)
# 1. ANSYS Fluent流场可视化基础

## 1.1 初识ANSYS Fluent流场可视化

在现代工程设计和科学研究中，ANSYS Fluent作为一个强大的计算流体动力学（CFD）软件，其流场可视化功能使得工程师和研究人员能够直观地理解流动现象，从而优化设计或加深对现象的理解。本章将探讨ANSYS Fluent的基础可视化功能，为深入学习和实际应用打下坚实的基础。

## 1.2 基于Fluent的流场可视化流程

流场可视化的核心流程包括：模型建立、网格划分、边界条件设置、求解计算以及后处理可视化。每一步都至关重要，其中后处理阶段尤为关键，它将计算所得数据通过色彩、纹理、矢量等多种方式直观地展示出来。

## 1.3 起步：Fluent中的基本操作

首先，用户需要在ANSYS Fluent中设置计算域，并导入或构建几何模型。通过网格划分工具对模型进行适当的网格划分后，接着定义边界条件、材料属性、流体属性等参数。最后运行求解器进行计算，计算完成后，便可以进入后处理阶段，利用Fluent提供的各种工具进行数据的可视化。

flowchart LR
A[模型建立] --> B[网格划分]
B --> C[边界条件设置]
C --> D[求解计算]
D --> E[后处理可视化]

在下一章节中，我们将进一步探讨流场数据处理的理论基础，帮助读者构建更为坚实的理论知识体系。

# 2. 流场数据处理理论基础

## 2.1 流体动力学的基本概念
流体动力学是研究流体运动规律及其与固体边界和其它流体相互作用的学科。理解这一领域中的连续性方程和动量方程，以及能量守恒和湍流模型，是流场数据处理的前提。

### 2.1.1 连续性方程和动量方程

连续性方程描述了流体质量守恒的定律。在微分形式中，对于不可压缩流体，可以表达为：

\nabla \cdot \mathbf{u} = 0

其中，$\mathbf{u}$ 是流体速度矢量。对于可压缩流体，连续性方程形式稍有不同，需要考虑密度变化：

\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0

其中，$\rho$ 是流体密度，$t$ 是时间。

动量方程，又称为Navier-Stokes方程，在笛卡尔坐标系下可写为：

\rho \left(\frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}\right) = -\nabla p + \mu \nabla^2 \mathbf{u} + \mathbf{f}

其中，$p$ 是流体压强，$\mu$ 是动力粘性系数，$\mathbf{f}$ 是体积力（例如重力）。

连续性和动量方程是流体动力学中最重要的基础方程，是流场分析和设计优化的关键。

### 2.1.2 能量守恒和湍流模型

能量守恒方程是基于热力学第一定律，对于无化学反应的流动系统，可以写为：

\rho c_p \left(\frac{\partial T}{\partial t} + \mathbf{u} \cdot \nabla T\right) = \nabla \cdot (k \nabla T) + \Phi

其中，$c_p$ 是定压比热容，$T$ 是温度，$k$ 是热导率，$\Phi$ 是由于粘性耗散产生的热量。

湍流模型用于模拟和解析流体的湍流运动。ANSYS Fluent 提供了多种湍流模型，包括 k-ε, k-ω, SST k-ω 等。不同的湍流模型有各自的适用范围和精度，对于工程应用需要根据具体情况进行选择。

## 2.2 数据处理技术概览

### 2.2.1 数据插值和网格生成

数据插值是后处理中常见的操作，用于在已知数据点之间估计新的数据值。线性插值是最简单的形式，适用于数据点较少且变化平滑的情况。更复杂的方法，如三次样条插值和多线性插值，则能提供更准确的结果。

网格生成技术在CFD（计算流体动力学）中至关重要。好的网格可以提高计算精度，减少计算资源消耗。网格类型包括结构化网格、非结构化网格和混合网格。通常使用如ANSYS Meshing工具生成网格，并需要对网格进行质量检查，例如检查网格的雅克比、倾斜度等指标。

### 2.2.2 数据平滑和噪声过滤

数据平滑技术用于减少数据中的噪声，提高数据可读性。常见的方法包括移动平均、高斯平滑和Savitzky-Golay滤波。移动平均法简单有效，但可能会损失数据的峰值信息；高斯平滑则使用加权平均，能更好保留边缘信息；Savitzky-Golay滤波则在平滑过程中保持数据的形状特征。

噪声过滤涉及将不规则的数据波动视为噪声并去除。这通常在后处理阶段进行，以改善可视化效果。在实际操作中，可以使用频域滤波，对数据进行快速傅里叶变换（FFT），在频域中过滤掉高频噪声分量，然后再通过逆变换恢复到时域。

上述内容为流场数据处理理论基础的第二章，从流体动力学基本概念到数据处理技术，为流场分析和可视化提供了坚实的基础。接下来的章节中，我们将深入探讨ANSYS Fluent的后处理技巧，并通过实践案例分析进一步理解理论知识的应用。

# 3. ANSYS Fluent后处理技巧

## 3.1 结果数据的提取与分析

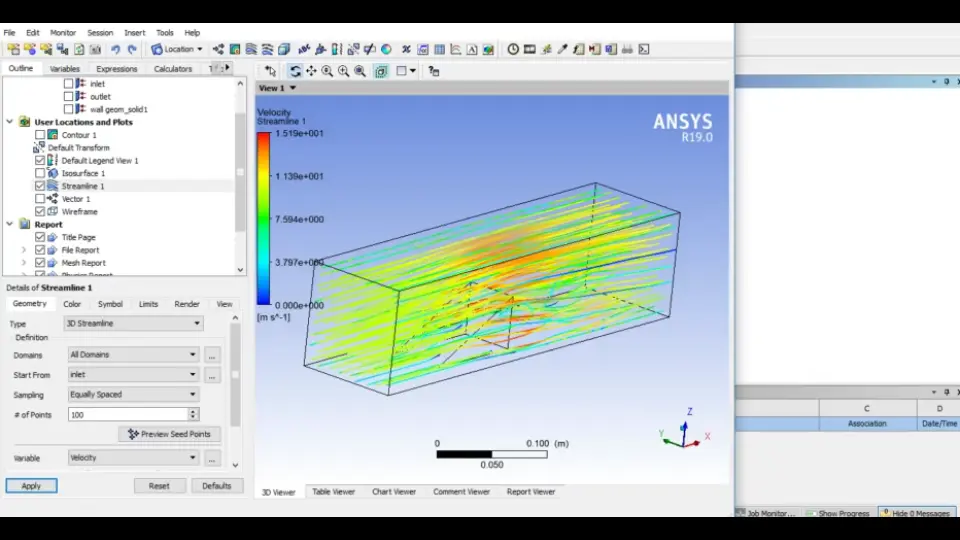
### 3.1.1 路径线和迹线的应用

在流体力学仿真中，路径线（Pathlines）和迹线（Streaklines）是分析流体流动模式的重要工具。路径线是表示在某一初始时刻，流体粒子的运动轨迹；迹线则表示在某段时间内，流体粒子的运动路径。在ANSYS Fluent中，路径线和迹线的生成对于理解复杂流动结构和流场中粒子的运动行为至关重要。

路径线和迹线可以通过以下步骤在ANSYS Fluent中生成：

1. 打开ANSYS Fluent软件，并加载相应的流场仿真案例。
2. 在结果菜单中选择Pathlines或S