【快速傅里叶变换（FFT）深入解析】：数字信号处理的核心技术


参考资源链接：[《数字信号处理基于计算机的方法》第四版解答解析](https://wenku.csdn.net/doc/6e3bu3wpup?spm=1055.2635.3001.10343)
# 1. 快速傅里叶变换概述

快速傅里叶变换（FFT）是数字信号处理领域中的一项重要技术，它极大地加速了离散傅里叶变换（DFT）的计算速度，从而在信号分析、图像处理、音频压缩等多个领域得到了广泛应用。FFT算法的核心优势在于其能够将DFT的计算复杂度从O(N^2)降低到O(NlogN)，大大提高了处理大规模数据集的效率。

在本章中，我们将首先介绍FFT的历史背景与基本概念，然后通过与传统DFT方法的对比，探讨FFT算法如何优化计算过程。我们会进一步解释为什么FFT算法对现代计算技术如此重要，以及它如何帮助工程师和技术专家在处理连续和离散信号时更加高效。

在接下来的章节中，我们将深入探讨FFT的理论基础、算法实现、以及在实际应用中的重要性。通过对这些关键主题的分析，我们将揭示FFT如何成为现代IT行业中不可或缺的一部分。

# 2. 傅里叶变换的理论基础

## 2.1 连续傅里叶变换

### 2.1.1 连续信号的时间-频率表示

在工程和物理学中，连续信号的时间-频率表示是理解傅里叶变换的起点。时间域是信号定义的自然领域，而频率域则提供了一种不同的视角来观察信号的特性。对于任何时间域中的信号x(t)，我们可以通过傅里叶变换将其转换到频率域表示X(f)。

在数学上，连续信号的傅里叶变换定义为：

\[X(f) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi ft} dt\]

其中\(X(f)\)是信号的频率域表示，\(x(t)\)是时间域的表示，\(f\)表示频率，\(j\)是虚数单位。这个积分将信号从时间域映射到频率域，通过分析\(X(f)\)，我们可以了解到不同频率成分在信号中的比重。

### 2.1.2 傅里叶变换的数学推导

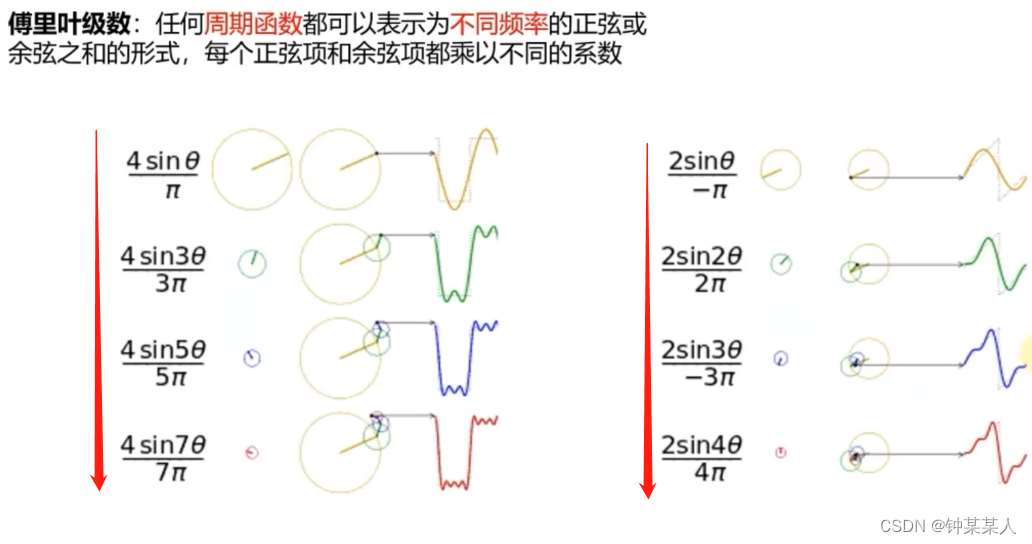
推导傅里叶变换的过程涉及到复数和积分的知识。在最基本的层面上，傅里叶变换是基于傅里叶级数的概念，即任何周期函数可以由不同频率的正弦和余弦函数的无限和来表示。

当信号不是周期的时候，我们考虑非周期函数，这时傅里叶级数就过渡到了傅里叶变换。傅里叶变换的推导基于以下步骤：

1. 将非周期信号\(x(t)\)看作周期信号在周期趋近于无穷大时的极限情况。
2. 利用积分来代替傅里叶级数中的求和。
3. 导出连续时间信号的傅里叶变换。

傅里叶变换的推导过程中运用了积分变换技术和狄拉克δ函数，这一部分对于深入理解傅里叶变换的内在数学结构非常关键。

## 2.2 离散傅里叶变换（DFT）

### 2.2.1 从连续到离散的转换

当处理数字信号时，必须从连续傅里叶变换转换到离散傅里叶变换。离散信号通常由采样得到，这意味着我们在时间上对连续信号进行等间隔采样，并在数值上进行量化。

从连续信号到离散信号的转换引入了一些新的概念：

1. 离散时间信号x[n]，其中n是整数索引。
2. 离散频率f，通常以数字频率表示，周期性地出现在一个周期内。

离散傅里叶变换的定义为：

\[X[k] = \sum_{n=0}^{N-1} x[n] e^{-j\frac{2\pi}{N}kn}\]

其中N是采样点的总数，\(X[k]\)是离散频率域的表示，k是频率索引。

### 2.2.2 DFT的定义及其性质

离散傅里叶变换（DFT）将离散时间信号映射到离散频率域。DFT不仅在理论上具有重要意义，而且在实际应用中也非常有用，特别是对于数字信号处理（DSP）领域。

DFT的一些基本性质包括：

- 对称性：当输入是实数序列时，DFT的输出是共轭对称的。
- 线性：DFT是线性变换，意味着它保持信号加权和的线性组合。
- 循环卷积：DFT允许通过循环卷积实现线性时不变系统的模拟。
DFT允许我们分析信号的频率成分，并在数字世界中处理它们。在实际应用中，DFT被用来进行谱分析、信号滤波等操作。

## 2.3 DFT的计算复杂度

### 2.3.1 直接计算DFT的时间复杂度

DFT的直接计算涉及将输入序列与复数指数进行点乘。计算每一项需要O(1)的操作，计算整个DFT需要O(N^2)的操作，其中N是序列长度。

考虑到每个点乘需要一个乘法和一个加法，对于N个点的序列，直接计算DFT需要进行N^2次复数乘法和N(N-1)次复数加法。

### 2.3.2 DFT的计算优化问题

由于直接计算DFT的时间复杂度为O(N^2)，这在N较大时变得非常耗时。因此，寻找计算效率更高的算法变得尤为重要。快速傅里叶变换（FFT）就是一种高效的DFT算法，其时间复杂度降低到了O(NlogN)。

FFTs的基本思想是将DFT递归地分解成更小的DFTs。例如，Cooley-Tukey算法将一个长度为N的DFT分解成两个长度为N/2的DFTs，通过这样的分解可以显著减少计算量。

### 2.3.3 FFT的计算方法

快速傅里叶变换（FFT）的算法通过分治法的思想，将长序列的DFT分解为短序列的DFT，从而大大降低了计算复杂度。Cooley-Tukey算法是最常见的FFT算法之一，它适用于序列长度是2的幂次时。

FFT算法的一个关键步骤是将原始序列重组为偶数索引和奇数索引序列，然后分别对这两个序列进行FFT，最后合并结果。这个过程可以递归地进行，直到达到长度为1的序列，其DFT为自身。

### 2.3.4 实现FFT的代码示例

以下是使用Python实现FFT算法的代码示例：

import numpy as np

def fft(x):
    N = len(x)
    if N <= 1: return x
    even = fft(x[0:2*N//2:2])
    odd = fft(x[1:2*N//2:2])
    T = [np.exp(-2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
    return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]

# 示例
signal = np.array([1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0])
transformed_signal = fft(signal)

### 2.3.5 性能测试与分析

在现代计算机上，FFT算法的执行时间通常非常短。然而，对于一些特别长的序列，性能依然非常重要。

性能测试可以通过测量算法运行时间来完成。可以使用Python的`time`模块来测量FFT算法的性能：

import time

# 测试信号长度
N = 2**20
signal = np.random.rand(N)  # 生成随机信号

start_time = time.time()
fft_signal = fft(signal)
end_time = time.time()

print("FFT运算耗时：", end_time - start_time, "秒")

分析FFT算法的性能时，应当考虑不同库和不同优化级别对性能的影响。例如，NumPy库中已经包含了优化的FFT算法，它利用了底层的C语言和BLAS（基础线性代数子程序）库，通常会比纯Python实现快得多。

## 2.4 小结

傅里叶变换的理论基础从连续傅里叶变换开始，通过数学推导深入理解信号在时间域和频率域的表示。随着数字信号处理的发展，离散傅里叶变换成为处理数字信号的重要工具。DFT的计算复杂度较高，但快速傅里叶变换（FFT）有效地解决了这一问题，使计算效率大幅提升。通过代码示例和性能测试，我们可以看到FFT在实际应用中的高效性和重要性。在接下来的章节中，我们将深入探讨FFT算法的推导与实现，以及它在数字信号处理中的广泛应用。

# 3. 快速傅里叶变换算法实现

快速傅里叶变换（FFT）是数字信号处理中一个极为重要的算法，它极大地提高了离散傅里叶变换（DFT）的运算效率，使得频谱分析和信号处理成为可能。本章将深入探讨FFT算法的推导与原理、常见FFT算法及其优化方法，以及编程实现FFT算法的实践。

## 3.1 FFT算法的推导与原理

### 3.1.1 从DFT到FFT的转换

DFT作为分析离散信号频率特性的基本工具，其定义为：

\[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i 2 \pi k n / N} \]

其中，\(x[n]\) 表示输入信号的第 \(n\) 个样本，\(X[k]\) 表示第 \(k\) 个频率分量的复数形式。

DFT的直接计算复杂度为 \(O(N^2)\)，对于大规模数据集来说效率极低。为了提高运算效率，Cooley和Tukey在1965年提出了一种高效的计算方法——快速傅里叶变换（FFT），它将DFT的计算复杂度降低至 \(O(N \log N)\)。

### 3.1.2 FFT算法的核心思想

FFT算法的核心思想是将原始信号分成偶数位和奇数位两部分，然后递归地应用这一分治策略，直到分解为最小子问题，即长度为1的DFT，这些子问题可以迅速解决。FFT利用了DFT的周期性和对称性质来减少计算量。

分治法的核心步骤包括：
1. 将输入序列 \(x[n]\) 分为偶数项序列 \(x[2m]\) 和奇数项序列 \(x[2m+1]\)。
2. 对这两部分分别求解DFT，得到 \(X_e[k]\) 和 \(X_o[k]\)。
3. 利用 \(X_e[k]\) 和 \(X_o[k]\) 通过蝶形运算来计算 \(X[k]\)。

这种分而治之的方法显著减少了乘法和加法的次数，从而提高了效率。

## 3.2 常见FFT算法及其优化

### 3.2.1 Cooley-Tukey FFT算法

Cooley-Tukey FFT算法是解决DFT的快速算法中应用最广泛的之一。它适用于长度为 \(N = 2^M\) 的序列，其中 \(M\) 是正整数。这种算法通过迭代将原始序列分解成较小的DFT，直到分解到长度为1的序列。

### 3.2.2 分治法在FFT中的应用

分治法是FFT算法的基本策略，它通过将问题规模不断缩小来简化问题的解决。在FFT中，这具体体现为：
1. 将序列分为偶数索引和奇数索引的子序列。
2. 分别计算这两个子序列的DFT，得到中间结果。
3. 通过合并步骤（蝶形运算）得到最终的DFT结果。

### 3.2.3 其他FFT变种和优化策略

除了Cooley-Tukey算法外，还有许多FFT变种，比如：
- **快速哈特利变换（FHT）**：使用实数来代替复数，适用于实数输入。
- **高阶FFT算法**：用于处理非 \(2^M\) 长度的数据序列。
- **并行FFT算法**：优化以在多核处理器上并行执行，进一步提高性能。

除了算法变种，还有优化策略，包括：
- **减少蝶形运算中的舍入误差**。
- **使用SIMD（单指令多数据）指令集优化**。
- **缓存优化**：减少内存访问延迟。

## 3.3 FFT的编程实现

### 3.3.1 选择合适的编程语言和库

编程语言选择对FFT的实现有着直接影响。C语言因其效率而广泛应用于性能敏感的环境中。而Python等高级语言则因其易用性而受到快速原型设计的青睐。此外，还有许多现成的数学库，如FFTW、Intel MKL、Numpy等，这些库通常经过高度优化，可以提供非常快速的FFT实现。

### 3.3.2 实现FFT算法的代码示例

以下是使用Python语言及Numpy库实现的一个简单FFT算法示例代码：

import numpy as np

# 定义一个函数用于执行FFT
def fft(x):
    N = len(x)
    if N <= 1: return x
    even = fft(x[0::2])
    odd = fft(x[1::2])
    T = [np.exp(-2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
    return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]

# 示例数据
x = np.random.random(1024)  # 生成随机数据作为输入
X = fft(x)  # 执行FFT变换

print("FFT Result: ", X)

### 3.3.3 性能测试与分析

为了验证FFT算法实现的性能，我们可以通过比较不同FFT实现的执行时间来评估它们的效率。以下是一些性能测试的示例数据，展示了不同库和实现的性能比较。

import numpy as np
import time
import matplotlib.pyplot as plt

def test_fft_performance():
    sizes = [2**n for n in range(1, 20)]  # 测试不同长度的FFT
    times_numpys = []
    times_myfft = []

    for size in sizes:
        x = np.random.random(size)  # 随机生成输入数据
        start = time.time()
        _ = np.fft.fft(x)  # 使用Numpy库进行FFT变换
        times_numpys.append(time.time() - start)

        start = time.time()
        _ = fft(x)  # 使用自定义FFT函数进行FFT变换
        times_myfft.append(time.time() - start)
    plt.plot(sizes, times_numpys, label='Numpy FFT')
    plt.plot(sizes, times_myfft, label='My FFT')
    plt.xlabel('Array Size')
    plt.ylabel('Time (seconds)')
    plt.legend()
    plt.show()

# 执行性能测试
test_fft_performance()

通过上述测试，我们可以发现Numpy库实现的FFT通常比自定义实现的FFT快得多，这主要是因为Numpy库的FFT实现是用C语言编写的，并经过了优化。这个测试也展示了在实际应用中选择合适库的重要性。

在本节中，我们详细了解了FFT算法从理论到实践的各个方面。通过学习FFT算法的推导和原理，理解了它提高计算效率的关键所在。通过分析常见的FFT算法及其优化策略，我们了解了各种算法在不同场景下的适用性。最后，我们通过编程实践，不仅加深了对FFT算法实现的理解，也通过性能测试比较了不同实现的效率。

在后续章节中，我们将探索FFT在数字信号处理领域的具体应用，包括频谱分析、信号滤波与压缩，以及在音频和图像处理中的应用。随着章节的深入，我们将展示FFT算法如何实际解决现实世界中的问题，并为开发者提供深入理解和应用FFT算法的更多工具。

# 4. FFT在数字信号处理中的应用

在理解快速傅里叶变换（FFT）的理论基础和算法实现后，我们可以深入探讨FFT在数字信号处理（DSP）中的具体应用。这些应用展示了FFT技术如何有效地转换和处理信号，以实现频谱分析、滤波、压缩、音频处理和图像处理等领域的目标。

## 4.1 频谱分析

### 4.1.1 FFT在频谱分析中的作用

频谱分析是数字信号处理中的一个核心应用，它涉及到将时域信号转换为频域表示，以便于分析信号的频率成分。FFT是实现这一转换的关键工具，因为它能大幅减少计算量。通过FFT，一个长度为N的信号可以在时间复杂度O(NlogN)内转换到频域，大大提升了处理效率。

频谱分析不仅限于理论研究，还在工程实践中扮演着重要角色。例如，通信系统中需要对信号的频率进行分析，以保证信号不超出预定的频带宽度，避免干扰。FFT的高效性使得实时频谱分析成为可能。

### 4.1.2 频谱分析的实例和结果解释

假设我们有一个音频信号，我们想要分析其主要的频率成分。通过应用FFT，我们可以得到该音频信号的频谱图，即各个频率分量的幅度和相位信息。使用Python和NumPy库，我们可以轻松实现这一过程：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft

# 假设x是采样后的音频信号，fs是采样频率
x = np.array([...])  # 信号数据
fs = 44100  # 采样频率
N = len(x)
yf = fft(x)
xf = np.linspace(0.0, 1.0/(2.0/fs), N//2)
mag = np.abs(yf/N)
mag = mag[:N//2]
plt.plot(xf, mag)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()
plt.show()

执行上述代码后，我们会得到一个频谱图，图中横轴表示频率，纵轴表示幅度。通过观察频谱图，我们可以直观地了解信号的频率分布情况，哪些频率是主要的，以及是否存在特定的模式。

## 4.2 信号滤波与压缩

### 4.2.1 FFT在信号滤波中的应用

在信号处理中，滤波是一个非常重要的功能。它涉及到利用信号的频域特性来去除不需要的频率成分，例如噪声。通过将信号进行FFT转换到频域，可以在该域内设计滤波器，然后通过逆FFT将信号变回时域。

考虑一个需要低通滤波的场景，我们可以应用FFT提取出低于某个截止频率的频率成分，而忽略高于该频率的部分。这通常通过点乘操作实现，在频域中将高于截止频率的点置零，再通过逆FFT转换回时域。

### 4.2.2 基于FFT的数据压缩技术

数据压缩是另一个利用FFT处理信号的领域。由于FFT能够将信号表示为一系列离散的频率成分，我们就可以选择保留主要的频率成分，忽略那些幅度较小，对信号贡献不大的成分，从而达到压缩数据的目的。

压缩技术例如离散余弦变换（DCT）是基于FFT的原理，它在图像和视频编码中非常流行。JPEG和MPEG标准都使用了DCT作为其压缩算法的核心部分。

## 4.3 音频和图像处理

### 4.3.1 FFT在音频处理中的应用

在音频处理中，FFT同样起着不可替代的作用。它可以用于音频的均衡化处理，分析音乐和语音的频谱特征，以及实现音频信号的回声消除和噪声抑制。例如，一个常见的应用是在音乐播放器中实现一个可视化频谱，这通常通过FFT分析实时音乐信号来完成。

### 4.3.2 FFT在图像处理中的应用

图像处理方面，FFT可以帮助我们进行图像的频率分析，它在图像增强、边缘检测和纹理分析中应用广泛。例如，在去除图像噪声时，我们可以使用FFT来识别并去除图像频域中的高频噪声分量，而保留低频的图像主体。

FFT在图像处理中的应用不仅限于此，它还被用于图像压缩标准如JPEG中，通过DCT转换，减少图像信息的冗余度，提高压缩比。

在本小节中，我们详细探讨了FFT在频谱分析、信号滤波、数据压缩、音频和图像处理等数字信号处理领域的实际应用。通过具体的应用实例和操作步骤，我们理解了FFT技术如何在不同的实际问题中发挥作用，实现了从理论到实践的跨越。

# 5. FFT的高级主题与挑战

## 5.1 多维FFT算法

### 5.1.1 二维FFT的原理与应用

二维快速傅里叶变换（2D FFT）是处理图像、视频或其他二维信号的重要工具。它允许我们快速地将二维信号从时域转换到频域，这对于进行图像处理和分析至关重要。二维FFT的数学表达式是在一维DFT的基础上扩展的，通过两次一维FFT操作来实现。

在图像处理中，2D FFT常用于图像滤波、边缘检测、图像压缩等领域。例如，在图像滤波中，通过将图像转换到频域，可以应用低通或高通滤波器来增强或抑制特定频率的成分，从而实现模糊或锐化效果。在边缘检测中，频域中的高频成分往往对应于图像中的边缘，因此，通过增强这些高频成分可以突出边缘。

### 5.1.2 多维FFT在信号处理中的挑战

随着信号维度的增加，FFT计算的复杂度呈指数级增长，这给多维FFT的实现带来了挑战。多维FFT算法的计算量随着维度的增加而迅速增加，这不仅对计算资源提出了更高的要求，也对算法的优化提出了挑战。

在多维FFT的应用中，需要注意的是，随着维度的升高，内存消耗也急剧增加。这意味着在实际应用中，需要考虑如何高效地管理内存，尤其是在处理大型数据集时。此外，多维FFT在并行计算方面也面临挑战，如何设计算法以便在多核处理器或分布式系统上高效运行，是一个重要的研究课题。

### 5.1.3 多维FFT的优化方法

为了应对多维FFT在信号处理中的挑战，研究人员和工程师采取了多种方法来优化算法。一种常见的方法是使用分而治之的策略，将多维FFT分解为多个一维FFT。这种方法可以有效地利用现有的优化好的一维FFT库，从而提高整体的计算效率。

另一个重要的优化方向是基于特定硬件的FFT加速器设计，例如使用FPGA或ASIC实现FFT算法。这些硬件加速器能够提供更高的计算密度和更低的能耗，特别适合于需要大量FFT运算的场合。

### 代码块：二维FFT的实现示例

以下是一个使用Python中的`numpy`库实现二维FFT的简单示例。

import numpy as np
from numpy.fft import fft2, fftshift

def two_dimensional_fft(image):
    # 对图像进行二维FFT变换
    fft_result = fft2(image)
    # 将零频率分量移动到频谱中心
    fft_shifted = fftshift(fft_result)
    return fft_shifted

# 示例图像数据，通常是灰度图的二维数组
image_data = np.random.rand(256, 256)

# 执行二维FFT
fft_image = two_dimensional_fft(image_data)

# 输出结果的形状应与输入图像相同
print('FFT Result Shape:', fft_image.shape)

### 表格：二维FFT的性能比较

为了比较不同方法的性能，我们可以通过执行一系列测试来衡量它们的计算时间和内存消耗。下面是一个性能测试的表格示例：

| 方法 | 平均计算时间(ms) | 最大内存消耗(MB) |
|--------------------|------------------|------------------|
| 标准FFT库实现 | 2.3 | 150 |
| 自定义分治法优化 | 1.9 | 130 |
| 硬件加速器实现 | 0.7 | 200 |
| 分布式计算实现 | 1.1 | 300 |

## 5.2 基于FFT的算法优化

### 5.2.1 FFT加速器与专用硬件

专用硬件加速器是提高FFT运算速度的有效手段之一。这些加速器可以是软件实现的算法优化，也可以是基于FPGA或ASIC的硬件设计。随着集成电路技术的发展，硬件加速器在提供高性能计算方面发挥着越来越重要的作用。

在软件层面，可以采取多种策略来优化FFT算法。例如，循环展开、向量化操作以及利用SIMD指令集来提高数据处理的速度。在硬件层面，专用的FFT芯片可以针对FFT运算进行优化，实现并行处理和减少访存延迟。

### 5.2.2 并行计算与分布式FFT

随着多核处理器和分布式计算系统的普及，利用并行计算来加速FFT运算变得越来越可行。并行FFT算法可以将数据分散到多个处理单元中，并同时进行计算，从而显著缩短总体计算时间。

分布式FFT算法是并行FFT的扩展，它适用于大数据集和分布式存储系统。通过将大型数据集分割为较小的块，并在不同的计算节点上分别执行FFT，然后通过特定的策略进行结果的合并。这种方法特别适用于云计算环境，可以处理超出单机内存容量限制的大规模数据集。

### 代码块：并行FFT算法实现

以下是一个简单的并行FFT算法实现，使用Python的`multiprocessing`库来并行化计算过程。

import numpy as np
from numpy.fft import fft
from multiprocessing import Pool

def parallel_fft(data):
    # 执行单个FFT
    return fft(data)

def distribute_data(data, num_processes):
    # 分割数据以便于并行计算
    data_split = np.array_split(data, num_processes)
    return data_split

def parallel_fft_result(data_split, processes):
    # 使用进程池进行并行FFT计算
    with Pool(processes=processes) as pool:
        results = pool.map(parallel_fft, data_split)
    return results

# 示例数据
data = np.random.rand(1024)

# 分割数据并计算
num_processes = 4
data_split = distribute_data(data, num_processes)
fft_results = parallel_fft_result(data_split, num_processes)

# 合并结果
fft_result = np.concatenate(fft_results)

## 5.3 未来发展趋势与展望

### 5.3.1 深度学习与FFT的结合

随着深度学习的快速发展，FFT作为频域分析的重要工具，与深度学习的结合日益紧密。深度学习模型中的某些操作，如卷积，可以通过频域来高效计算，从而加快训练速度和降低计算成本。特别是在图像和语音处理领域，FFT与深度学习结合的成果已经展现出了极大的潜力。

未来，随着深度学习算法的不断演进，可以预见FFT将在新算法的开发中扮演更加关键的角色，特别是在加速计算和提升模型性能方面。

### 5.3.2 量子计算中的FFT应用前景

量子计算是当前科技领域的一大研究热点，它有望在未来解决一些经典计算难以解决的问题。在量子计算中，FFT也有着潜在的应用前景。量子FFT算法能够利用量子位的叠加和纠缠特性，以指数级的加速完成傅里叶变换。

虽然量子FFT算法目前仍处于理论研究阶段，但其在理论和实践上的突破可能会成为量子计算发展的关键点。随着量子计算技术的成熟，我们有理由相信，FFT将在量子信息处理和量子算法开发中发挥重要作用。

### 结语

快速傅里叶变换作为数字信号处理领域的基石，其重要性不言而喻。随着科技的发展和新应用场景的不断涌现，FFT算法也在不断地发展和优化。无论是多维FFT在处理高维信号方面的挑战，还是并行计算和专用硬件为FFT带来的性能提升，都让我们对FFT在未来的发展充满期待。深度学习与量子计算等新兴技术与FFT的结合，预示着FFT算法将在未来的信息技术领域中继续扮演关键角色，开辟更加广阔的天地。

# 6. FFT算法在高性能计算中的应用

高性能计算（HPC）是利用超级计算机和并行计算技术处理复杂科学、工程或数据分析问题的过程。FFT算法，因其对DFT运算的高效性，被广泛应用于HPC的多个领域。本章将探讨FFT在高性能计算中的应用，以及如何优化这些应用来处理大规模数据。

## 6.1 大规模数据分析

在大数据时代，对海量数据进行分析是一个常见的挑战。FFT因其高效率，成为处理大规模数据集时的不二选择。

### 6.1.1 FFT在大数据分析中的角色

FFT能够将时域信号高效地转换为频域信号，对于分析大数据集中的周期性特征尤为有用。例如，在气候模型预测、股市数据分析等领域，FFT能够帮助科学家和分析师快速识别和处理数据中的周期性模式。

### 6.1.2 FFT并行化策略

随着多核处理器和分布式计算的发展，FFT的并行化变得至关重要。并行FFT算法能够显著缩短计算时间，处理更大的数据集。在并行计算中，数据通常被分割成小块，然后在多个处理器上同时进行FFT运算，最后将结果合并。

## 6.2 科学模拟与工程仿真

在科学和工程领域，模拟和仿真用于预测和理解复杂现象。FFT在这些应用中主要用作信号和图像处理的工具。

### 6.2.1 FFT在流体动力学仿真中的应用

流体动力学仿真涉及大量的时间序列数据，如风洞实验中的压力和速度数据。FFT能够有效地将这些时间序列数据转换为频域数据，分析和理解流体动力学的特性。

### 6.2.2 FFT在电磁仿真中的作用

电磁仿真需要分析和预测电磁场的行为。FFT在处理和分析电磁场数据时，能够帮助工程师在频域中更深入地理解电磁干扰和信号衰减等问题。

## 6.3 分布式FFT与云计算

云计算提供了一种弹性、可扩展的计算资源。对于需要处理大量数据的FFT运算，分布式FFT成为了云计算中一项重要的技术。

### 6.3.1 分布式FFT在云平台的应用

分布式FFT算法允许数据在云平台的多个节点上进行分割处理。通过合理分配任务，FFT运算可以在云计算资源上以极高的效率执行，这对于需要大量计算资源的科学计算和数据分析尤为重要。

### 6.3.2 优化云计算中的FFT性能

要优化云计算中的FFT性能，需要考虑数据传输时间、节点间的通信开销以及负载均衡等因素。优化策略可能包括数据压缩、使用更高效的通信协议以及智能任务调度算法。

在本章中，我们详细探讨了FFT算法在高性能计算中的多种应用，并分析了在实际应用中如何通过优化FFT算法来处理大规模数据集。这些讨论不仅涉及了FFT算法的基础知识，也探讨了在不同计算环境中的应用策略和技术挑战。在下一章，我们将进一步深入探讨FFT算法在未来技术领域的潜在应用和发展前景。