【数字信号处理算法优化】：提升处理速度与效率的策略


参考资源链接：[《数字信号处理基于计算机的方法》第四版解答解析](https://wenku.csdn.net/doc/6e3bu3wpup?spm=1055.2635.3001.10343)
# 1. 数字信号处理基础

## 1.1 信号的数字化过程
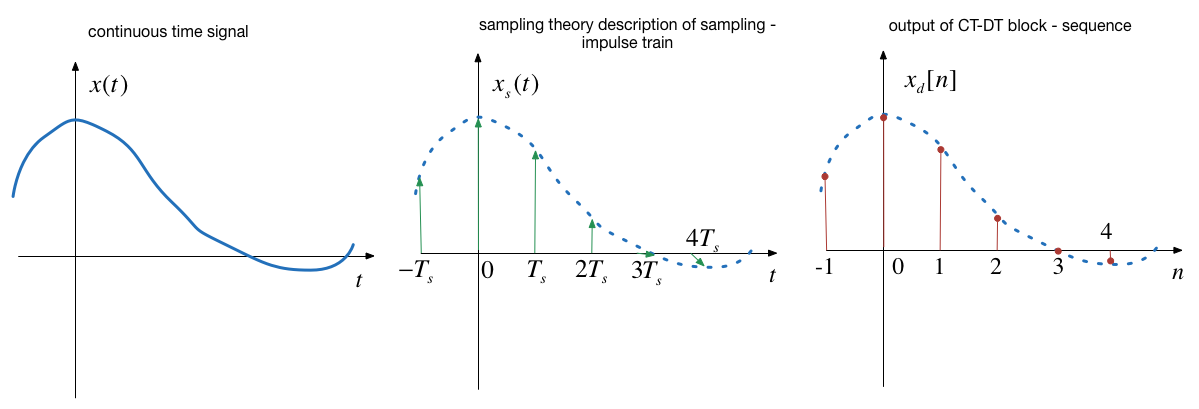
数字信号处理（DSP）是通过数字系统处理连续信号的技术。在开始处理之前，我们需要将模拟信号转换为数字形式。这一过程称为数字化，涉及两个基本步骤：采样和量化。采样是每隔一定时间间隔对模拟信号进行测量，量化则是将测量值转换为数字表示的过程。理解这两个步骤对于数字信号处理至关重要，它们是数字系统能够理解和处理信号的先决条件。

## 1.2 离散时间信号与系统
在数字信号处理中，我们经常处理的是离散时间信号，这些信号在时间上是一系列间隔均匀的点。与连续信号相比，离散信号更容易被计算机处理。离散信号可以用数学表达式表示，例如序列和矩阵。此外，数字信号处理还涉及到离散时间系统，包括它们的实现方式（如有限脉冲响应（FIR）和无限脉冲响应（IIR）滤波器）以及它们的特性（如线性时不变系统）。

## 1.3 傅里叶变换的基本概念
傅里叶变换是数字信号处理领域中的一个核心概念，它允许我们将信号从时域转换到频域。频域表示提供了关于信号频率成分的信息，这对于许多应用来说非常有用，比如信号分析、噪声消除和信号压缩。理解傅里叶变换的基本原理和其逆变换对于设计有效的数字信号处理算法是必不可少的。我们将从离散时间傅里叶变换（DTFT）开始，逐步深入到更为实用的快速傅里叶变换（FFT）。

# 2. 算法优化的理论基础

算法优化是计算机科学中一个不断追求卓越的领域，它涉及到对程序执行效率的提升，以及对系统资源使用的最佳化。随着数据量的爆炸性增长和处理需求的日益复杂，算法优化显得尤为重要。本章将详细探讨算法优化背后的理论基础，包括算法复杂度分析、性能瓶颈的识别和优化策略的制定。

## 2.1 算法复杂度分析

### 2.1.1 时间复杂度和空间复杂度的概念

算法复杂度是衡量算法性能的核心指标，它主要分为时间复杂度和空间复杂度。

- 时间复杂度是指完成一个算法所需要的计算步骤的数量。通常，算法时间复杂度用大O表示法来描述，它表示随着输入规模的增加，算法执行时间的增长趋势。

- 空间复杂度则是指执行一个算法所需要的存储空间量。它通常与算法所需的最大内存量有关，并与输入数据的规模成正比。

### 2.1.2 理解大O表示法

大O表示法是一种数学符号，用来描述一个算法的运行时间与输入数据量n之间的关系。我们通常使用它来分类和比较算法的效率。

例如，一个简单的线性搜索算法，其时间复杂度是O(n)，表示算法的运行时间与输入数据的数量线性相关。如果我们有一个二分搜索算法，它的时间复杂度则是O(log n)，表示算法的运行时间随着输入数据量的增加呈对数增长，这通常意味着该算法比线性搜索更高效。

## 2.2 常见的性能瓶颈

### 2.2.1 CPU和内存限制

算法性能的提升常常受到硬件资源的限制，尤其是CPU和内存。在多任务处理环境中，CPU时钟周期和内存容量成为影响程序运行效率的关键因素。

- 对于CPU限制，可以通过优化算法来减少不必要的计算，使用更快的指令集，或者并行化处理来突破单核处理的瓶颈。

- 在内存使用方面，我们可以通过优化数据结构来减少内存占用，或者设计更为有效的内存管理策略，比如内存池等。

### 2.2.2 I/O延迟与吞吐量问题

除了CPU和内存之外，输入/输出（I/O）的延迟和吞吐量也是常见的性能瓶颈。尤其是在涉及到大规模数据读写时，I/O操作的延迟可以显著影响程序的整体性能。

- 解决I/O延迟的方法包括使用缓存、异步I/O、或者改进数据存储的布局，以减少寻址时间和提高数据传输效率。

- 为了提升吞吐量，可以采用多线程或异步处理来隐藏I/O延迟，或者通过优化算法减少I/O操作的频次。

## 2.3 算法优化的基本策略

### 2.3.1 空间换时间

当算法执行时间过长时，可以考虑使用更多的内存来存储中间结果，从而减少计算时间。例如，通过预计算部分结果并将它们存储起来，可以在后续步骤中快速访问，这就是所谓的“记忆化”（memoization）技术。

### 2.3.2 时间换空间

相对地，当内存使用过量时，可以优化算法以减少内存的使用，哪怕是以牺牲一些执行时间为代价。例如，在排序算法中，归并排序比快速排序使用更多的栈空间，但是快速排序则可能更慢，因为它有更多的递归调用。

### 2.3.3 并行计算与多线程

现代计算机系统通常拥有多个核心，使用并行计算或多线程技术可以有效利用这些资源。并行算法设计需要考虑如何将问题分解成多个可以同时解决的子问题，并协调这些子问题的解决过程。

本章节通过介绍了算法优化的基础理论，从算法复杂度分析到性能瓶颈，再到优化策略，为后续章节的实践技巧和应用案例打下了坚实的基础。下一章将着眼于实践中如何应用这些理论，通过具体的技术和方法来提升算法的实际性能。

# 3. 实践中的优化技巧

## 3.1 循环优化技术

循环是程序中最为常见的结构之一，尤其在数字信号处理领域，循环结构更是承担了绝大多数的计算任务。通过对循环进行优化，可以显著提高算法的执行效率和性能。

### 3.1.1 循环展开与合并

循环展开是将循环体中的若干次迭代合并为一次迭代，以减少循环控制的开销。例如，如果一个循环每次迭代执行的操作很少，那么循环控制指令可能就占用了大部分的执行时间。通过循环展开，可以减少这些开销。

// 循环展开示例
for (int i = 0; i < 100; i += 2) {
    a[i] += b[i];
    a[i+1] += b[i+1];
}

在上述代码中，我们通过每次迭代处理两个数组元素的累加操作，将原本100次的循环控制降低到50次。循环展开可以通过手动编写代码实现，也可以利用现代编译器的优化选项，如GCC的`-funroll-loops`选项自动完成。

循环合并则是将两个或多个具有相同迭代步长和迭代次数的循环合并为一个循环。这通常用于减少循环控制的开销，以及提高缓存利用率。

### 3.1.2 循环无关代码外提

循环无关代码外提（Loop-Invariant Code Motion）是一种编译器优化技术，指的是将循环体外的计算（即循环不变量）移动到循环之外。在手动优化时，开发者应仔细检查循环体内是否存在不必要的重复计算。

// 循环无关代码外提示例
for (int i = 0; i < N; ++i) {
    temp = a[i] * b