可靠性分析:Bang-Bang鉴相器在全数字锁相环设计中的稳定性研究(长期使用稳定性保障)
发布时间: 2024-12-16 20:22:30 阅读量: 2 订阅数: 7 


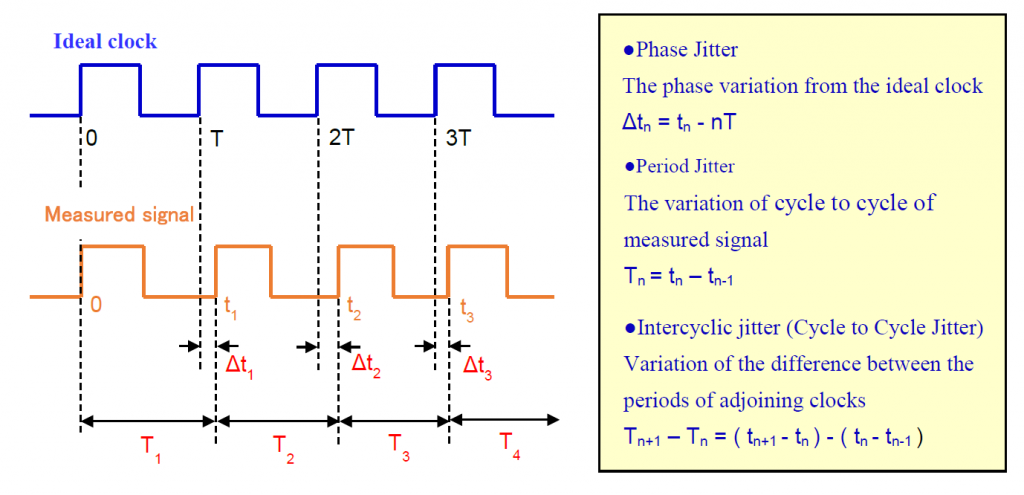
一种基于Bang-Bang鉴相器的全数字锁相环的设计
参考资源链接:[全数字锁相环设计:Bang-Bang鉴相器方法](https://wenku.csdn.net/doc/4age7xu0ed?spm=1055.2635.3001.10343)
# 1. Bang-Bang鉴相器与全数字锁相环概述
在现代通信系统中,频率合成和相位同步是关键技术。Bang-Bang鉴相器因其高速、高动态性能和简单性,在全数字锁相环(Digital Phase-Locked Loop, DPLL)中扮演着核心角色。它为实现精确的相位跟踪与快速锁定提供了可能。
## 1.1 全数字锁相环的重要性
全数字锁相环是现代数字通信接收机的关键组件,它能够实现对载波频率和相位的精确跟踪,从而保证数据的准确解调。与传统的模拟锁相环相比,DPLL具有更好的灵活性、可编程性和稳定性。
## 1.2 Bang-Bang鉴相器的作用
Bang-Bang鉴相器是DPLL的核心部件之一,它通过比较输入信号与本地振荡信号之间的相位差异,并产生相应的控制信号来调整本地振荡频率。这种方法在确保快速锁定的同时,也能在强噪声环境中保持良好的性能。
接下来的章节将详细探讨Bang-Bang鉴相器的工作原理和性能指标,以及全数字锁相环的设计细节和性能优化方法,为读者提供深入理解这一领域的机会。
# 2. Bang-Bang鉴相器的基本原理与性能分析
## 2.1 Bang-Bang鉴相器的工作原理
### 2.1.1 鉴相器的功能与作用
Bang-Bang鉴相器是一种数字鉴相器,它主要应用于锁相环(PLL)系统中,用于比较参考信号和反馈信号的相位差,并输出相应的控制信号。Bang-Bang鉴相器的核心功能是确定相位差的方向和大小,进而在锁相环路中生成误差电压,用以驱动压控振荡器(VCO)调整频率,以实现锁定。
鉴相器的作用在锁相环中不可或缺,它直接关系到环路能否快速准确地锁定目标频率,以及在锁定后能否保持稳定。由于其简单性和高可靠性,Bang-Bang鉴相器在高速数字通信系统中得到了广泛的应用。
### 2.1.2 Bang-Bang鉴相器的信号处理
在Bang-Bang鉴相器中,信号处理主要是通过比较两个输入信号(参考信号和反馈信号)的相位,输出一个代表相位差方向的二进制信号(±1)。当参考信号相位超前于反馈信号时,鉴相器输出+1;相反,当参考信号相位滞后于反馈信号时,输出-1。这种二值化的输出方式使得Bang-Bang鉴相器具有高动态响应和良好的抗噪声特性。
这种信号处理方法允许锁相环对快速变化的相位差做出迅速反应,从而提高了系统的锁定速度和稳定度。然而,由于其输出是离散的二进制值,Bang-Bang鉴相器可能会引入更多的噪声,这需要在设计中考虑适当的滤波和积分策略。
## 2.2 Bang-Bang鉴相器的性能指标
### 2.2.1 稳定性与跟踪性能
稳定性是Bang-Bang鉴相器的首要性能指标之一,它决定了锁相环是否能够在一个稳定的频率上运行,以及在外界条件发生变化时能否保持锁定状态。Bang-Bang鉴相器的稳定特性与鉴相特性密切相关,理想的鉴相器应能够提供准确的相位误差信息,以便锁相环能够快速响应并适应频率变化。
在实际应用中,Bang-Bang鉴相器需要具备较高的跟踪性能,意味着能够有效地追踪高速变化的相位差。这通常需要环路滤波器具有较高的通频带宽度,并且Bang-Bang鉴相器本身要有良好的动态特性,以实现快速锁定和维持稳定跟踪。
### 2.2.2 噪声特性与误码率
噪声特性对于任何通信系统的性能都是至关重要的,对于Bang-Bang鉴相器而言,它主要受到鉴相器输出的噪声和环路滤波器的噪声抑制能力的影响。Bang-Bang鉴相器中的噪声包括相位噪声和量化噪声,这些噪声都会对系统的误码率(BER)产生负面影响。
误码率是衡量通信系统性能的一个关键指标,它描述了在传输或处理信号过程中发生错误的概率。对于Bang-Bang鉴相器,良好的噪声性能可以降低误码率,从而提高数据传输的准确性。在设计时,需要通过合理设计滤波器参数和鉴相器算法来最小化噪声对系统性能的影响。
## 2.3 Bang-Bang鉴相器的数学模型
### 2.3.1 数学模型的构建
为了分析和优化Bang-Bang鉴相器的性能,构建一个准确的数学模型是至关重要的。Bang-Bang鉴相器的数学模型通常包括离散时间模型和连续时间模型,其中离散时间模型更适合数字实现。
在构建数学模型时,需考虑信号的相位差以及系统对相位差的响应特性。例如,可以假设鉴相器的输入信号为正弦波信号,其相位差为动态变化的值,并通过建立差分方程来描述鉴相器的响应。此外,模型中还需考虑可能的噪声源,包括量化噪声、热噪声等,这些噪声将通过特定的函数形式被融入模型中。
### 2.3.2 模型在稳定性分析中的应用
数学模型在Bang-Bang鉴相器的稳定性分析中扮演着核心角色。通过数学模型,我们可以进行系统的线性稳定性分析,推导出锁相环的稳定条件,并预测在特定参数设置下系统的响应行为。
例如,使用线性化技术,可以将鉴相器的非线性特性简化为线性特性,然后应用经典的控制理论方法,如根轨迹法和波特图,来分析系统的稳定性。此外,通过仿真和实验验证数学模型预测的稳定性结果,可以对鉴相器的性能进行进一步的优化和调整。
```mathematica
(* 这里用Mathematica代码块模拟Bang-Bang鉴相器的数学模型的建立和求解过程 *)
(* 给出一个假设的鉴相器输入信号和反馈信号的数学表达式 *)
input = Sin[2 Pi f t];
feedback = Sin[2 Pi f (t - PhaseError)];
(* 假设鉴相器的行为可以通过一个简单的差分方程来描述 *)
鉴相器输出 = Sign[feedback - input];
(* 建立描述相位差动态的差分方程 *)
PhaseError = α *鉴相器输出 + ε; (* 其中α为比例系数,ε为噪声项 *)
(* 通过数值方法求解差分方程,研究系统行为 *)
NDSolve[{D[PhaseError[t], t] == α *鉴相器输出 /. {鉴相器输出 -> Sign[feedback - input]}, PhaseError[0] == 0}, PhaseError, {t, 0, T}]
```
以上代码块使用Mathematica语言构建了一个简化的Bang-Bang鉴相器数学模型,并通过差分方程描述了相位误差的变化。代码中的`NDSolve`
0
0





